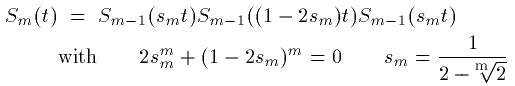第7章 指数作用素のフラクタル分割(後編)

より安定な分解法

先の方法により無限次のSymplectic Integratorが構築されるのですが 同じ次数のSymplectic Integratorによる計算でも、エネルギーの振動を より押えた安定なSymplectic Integratorを構築することができます。

(31)式でのExp(t(A+B))の 恒等分解を更に複雑な形で恒等 分解することにより、その安定なSymplectic Integratorが構築されます。

変形の仕方にはいろいろあるのですが、例えば(35)式を複雑化して

(36)

と再帰定義する分解方法があります。この方法の明瞭な利点は s_mが実数であるため物理計算に即実用可能なことです。
また分割の形が前後でSymmetric(対称)です。時間推進作用素であるこの 作用素がSymmetricであると、時間反転に対して対称となります。 つまりS_m(t)S_m(-t)=1 となります。この種の分割をSymmetric Decompsitionと呼びます。

さらに別な形式の変形として鈴木先生が推奨されている次の分割を 紹介します。

(37)

これもSymmetric Decompsitionです。1次あげることで指数の項の数が 約5倍になるので計算量が著しく多くなるのが困りますが、数値積分の 精度が遥かにあがります。

下図に(36)式型と(37)式型の分解によるSymmetric数値積分の結果を 載せます。Hamitonianなどの系の条件は (00)式で例示したものと同じです。


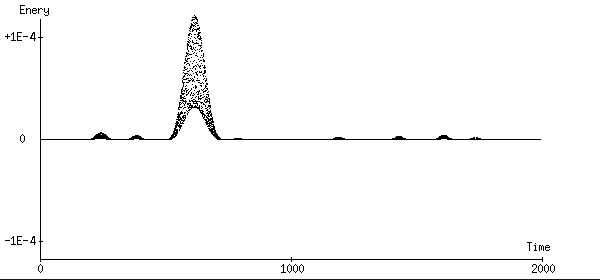
3項分解型3次Symplectic法：計算にかかった時間は 130秒です。


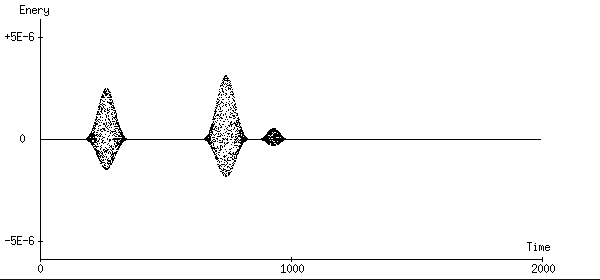
5項分解型3次Symplectic法：計算にかかった時間は 180秒です。 振動の振幅が3項型のものよりさらに20分の1になっています。

2m-1奇数次精度と2m偶数次精度の関係

Symmetric Decompsitionのうち奇数次の分解S_{2m-1}(t) についてさらに考えます。元の指数とこの分解との関係は次の通りです。

(38)

ここでR_2m(A,B)は、S_{2m-1}(t)の不正確さ のうちt^{2m}の項のA,Bによる多項式の係数を 表します。このR_2m(A,B)の意外な性質を調べます。

(38)式のtを-tに反転した式を用意して それと(38)式の辺辺を掛け合わせます。S_{2m-1}(t)が Symmetric Decompsitionであることを考慮すると

(39)

となります。t=0を代入してもこの式は成り立つはずなので 結局 R_2m(A,B)=0となってしまいます。

(38)式を見直せば、S_{2m-1}(t)にはt^{2m}の 不正確さがないことがわかります。つまり2m-1次の分割 S_{2m-1}(t)は実は2m次の分割も兼ねるのです。

これにより(37)式のタイプの分解法は次のように拡張されます。

(40)

このタイプの分解法ではS_1(t),S_2(t)は共に(30)式を 用います。偶数次分割の2次おきに高次の分解を作るので、指数の総数が格段に 少なくなります。

フラクタル分解

(40)式で示される各次数の指数積展開での各項の展開係数をコンピュータで計算します。
Symplectic Integratorでのこの展開係数の意味は、短い時間ステップ Δtうちの各係数の分を作用素 A(=Du),B(=Dk)のどちらか 一方だけで時間発展するという意味です。2種の作用素があるので 時間はのべ2Δt進めることになります。
各係数の指数ひとつを作用する作業を1stepとして、 各stepで時間がどのように進んでいくかを以下の図に示します。

4次分解S_4(t)

6次分解S_6(t)

8次分解S_8(t)

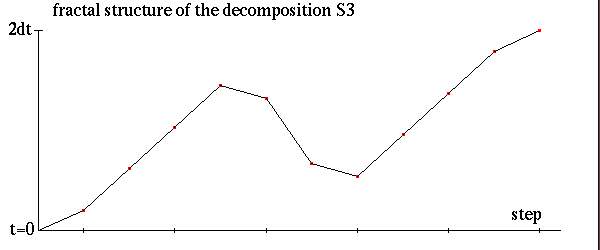
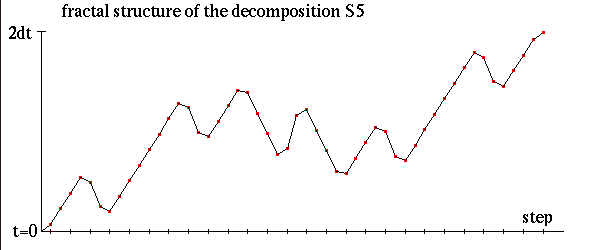
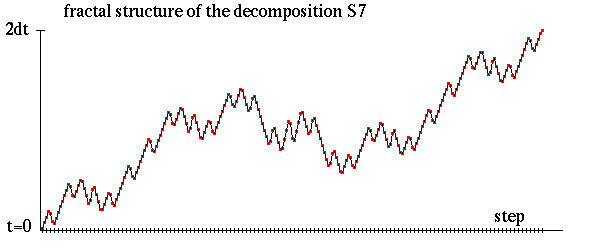
次数があがるとこのように折れ線グラフがより複雑になります。 その複雑さの入り組み方はまさにfractal的です。 高次分解が低次分解を再帰的に組みあわせていることからも その構造がfractalになることは察しがつきます。

このような性質からこの指数作用素の分解はfractal decomposition と命名されました。

  • 第8章 分解係数を作成するプログラム
  • 目次
    Copyright(C) by Naoki Watanabe. Oct 21st, 1995.
    渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp