第6章 指数作用素のフラクタル分割(前編)
より高次のSymplectic Integratorを構築するには(15)式
の指数積展開をより細かく分割しなくてはなりません。例として
指数4項(実質3項)からなる2次の分割を(16)-(22)式に示しましたが
たった2次でも計算がこれほど面倒です。この方法で
高次の分割を求めるのは非常に困難です。
1990年にこの分割を容易に無限次まで行う画期的な方法が
鈴木増雄先生(当時 東京大学理学部物理学科教授、現 同名誉教授 東京理科
大学教授)によって考案されました。この分割により細分化された時間
ステップの様子にフラクタルの性質があることからFractal Decomposition
(フラクタル分割)と命名されました。
この章ではこのフラクタル分割の理論について解説します。
指数作用素の分割のおさらい
非可換な作用素 A,B の和の指数にはスカラーの指数分解
公式が成り立ちません。そのためこの指数を個々の作用素の指数の
積として表すためには(15)式の無限積展開とならざるをえません。
tのm次までの展開で分割します。
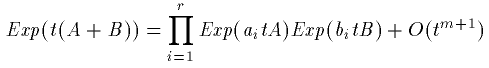 (27)
(27)
この指数の積の数 rはm次分割が得られるように
調整されます。各指数の係数 a_i,b_iを決定することが
この展開作業の主題です。
Πの部分を以後 S_m(t)と表すことにします。
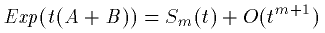 (28)
(28)
S_1(t)は、明らかに
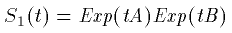 (29)
(29)
です。S_2(t)は、(22)式の通り
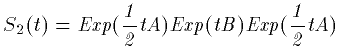 (30)
(30)
です。
2次分割による3次分割の構成
S_3(t)を求めるには少々工夫が必要です。この工夫が鈴木先生が
思い付かれた方法です。
まずExp(t(A+B))を次のようにある定数sを
用いて書き改めます。
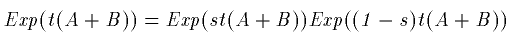 (31)
(31)
作用素(A+B)と(A+B)は可換なのですから、
この等式は近似ではなく厳密な恒等式です。
(31)式の右辺の2つの指数のそれぞれをtの3次の項まで
Tylar展開します。そしてこの3次の項が全体の指数積に及ぼす
影響を考えると、それはこの2つの3次の項の和であることに
気が付きます。つまり
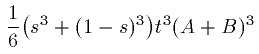 (32)
(32)
の項のことです。もしこの項が0になるのなら、それは(31)式の
2つの指数のそれぞれのtの3次の項は全体の指数積に
なんら影響を及ぼさないことになります。つまりこれらに誤差が
含まれていても全体ではその誤差はなくなるのです。全体が
3次となり4次の項で始めて誤差がでるのです。
(32)式の項が0になる条件は明らかに
 (33)
(33)
です。このとき(31)式の2つの指数をそれぞれ2次のS_2(t)
で表すと、全体は3次になることはもうおわかりでしょう。
結局、
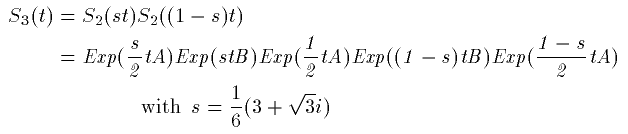 (34)
(34)
となります。これで3次の指数積分割はできあがりです。
m-1次分割によるm次分割の構成
一般にm次の分割を考えます。m-1次の
それが求まっているとしてこれを用いて再帰的にm次を
構成します。
(31)式の2つの指数をそれぞれm-1次のS_{m-1}(t)
で表して、S_{m-1}(t)が持つm次の不正確さが
全体に現れないように、sを調整します。
すなわち次の通りです。
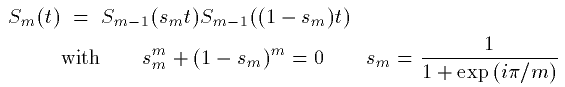 (35)
(35)
こうして再帰的に無限の精度まで高次の指数積分解が可能なのです。
各指数の係数a_i,b_iはこの方法によりコンピュータで簡単に
求まります。
第7章 指数作用素のフラクタル分割(後編)
目次
Copyright(C) by Naoki Watanabe. Oct 21st, 1995.
渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp
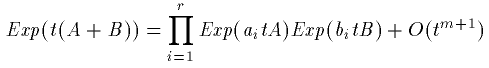 (27)
(27)