を求めるには、上式をExpの定義にしたがって
テイラー展開し、作用素の同じ項でまとめ、その係数を比較し、
u_i,k_iの連立方程式を作り、それを解くことによって得られます。
試しに一つ例として求めてみましょう。有限積で、さぼって r=2
とします。さらにt の3乗のオーダーを無視することにします。
(15)式は
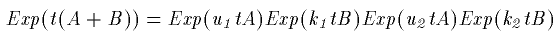(16)
となります。この左辺は
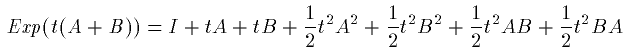(17)
と展開されます。右辺は少し込み入ってますが、t^3 を無視して
計算をすすめます。
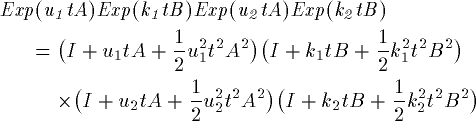
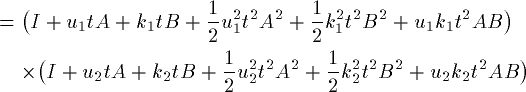
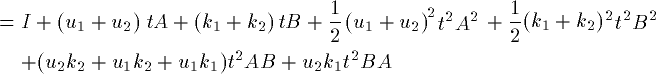(18)
これから係数を比較して、u_i,k_iの連立方程式を作ります。
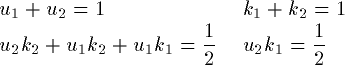(19)
独立でない方程式があるのでこれだけでは係数は一意には
定まりませんが、これは我々に係数を選ぶ権利があることになります。
なので展開が最も簡単になるように k_2=0 としましょう。
こうすると解は次のようになります。
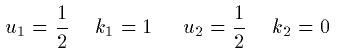(20)
が求まりました。
よって(15)式の2次近似式は
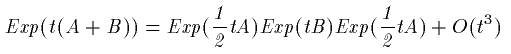(21)
となります。指数の並び方が左右対称になっていますね。
実はこの対称性が後で重要になります。そのため先程、
k_2=0 を選んだのです。
この結果を(04)式に用いると、
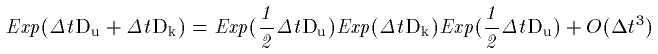(22)
作用素が分解されたので具体的な計算にはいれます。
まず最初の作用素による変換で (p(0),q(0)) が
(p_1,q_1) に写ります。
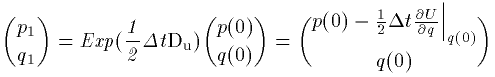(23)
次の作用素による変換で (p_1,q_1) が (p_2,q_2)
に写ります。
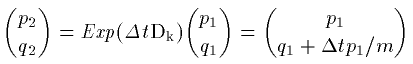(24)
最後の作用素による変換で (p_2,q_2) が
(p(Δt),q(Δt)) に写ります。
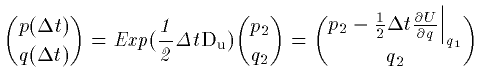(25)
こうして1つの時間ステップ \Delta t を進めることができました。
以上のプロセスで運動方程式を解いていく方法を
2次のSymplectic解法と呼びます。
第5章 影のHamiltonian
目次
Copyright(C) by Naoki Watanabe. Oct 21st, 1995.
渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp
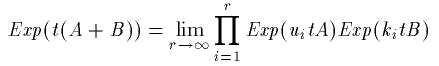(15)