第3章 微分作用素の分割
次にこの Exp{Δt D} という謎の作用素が具体的に
どのようなものなのかを調べてみましょう。
D はH から決まる作用素です。H は
運動エネルギー K とポテンシャルエネルギー Uと
の和でした。よって作用素D も K による要素と
U による要素の和になるのです。
つまり、それぞれを、Du Dk とすれば、
D = Du + Dk
と分けられるということです。
スカラーの指数関数の法則 exp{A+B}=exp{A}exp{B} が
この作用素の指数に対しても成り立つとしたらどうなるでしょう。
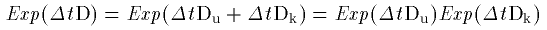 (09)
(09)
これが成り立てば、(04)式は
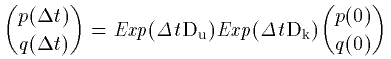 (10)
(10)
となります。
つまり、(p(0),q(0)) を Exp(Δt Dk)で変換した
ものをさらに Exp(Δt Du) で変換することになるのです。
では、この Exp(Δt Dk) (p(0),q(0)) とは、具体的に
何なのでしょう?
Dk は、U が無い系での H が作る
作用素 D です。つまり自由粒子というわけです。
自由粒子ならばその運動の計算は簡単かつ厳密です。
運動量は変化しないで、位置が一定方向に変化するだけですから。
なので、Exp(Δt Dk)(p(0),q(0)) が表すベクトルは
粒子を自由粒子としてΔt後の状態まで積分しているのです。
自由粒子の運動なので、積分は厳密に行われます。この厳密な積分が
Symplectic法の鍵となっています。
結局、作用素 Exp(Δt Dk) の効果は次式で表されます。
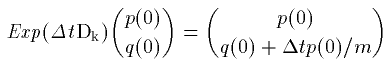 (11)
(11)
次に、Exp(Δt Du)(p(0),q(0)) について同様に考えます。
D_u は、K がない H の Dです。
運動エネルギーがないというのは意味がわかりませんが、Uだけ
なので、運動方程式より位置 q が変化しないで、運動量
p だけが変化していることになります。q が変化しない
とU が変わらないので p の変化は一定になります。
よってこれも自由粒子と同じ様に積分が厳密にできます。その効果は
次式で表されます。
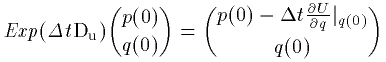 (12)
(12)
このように、作用素 Exp(Δt D) が Exp(Δt Dk)
と Exp(Δt Du) の積に分離できると、個々の作用素は粒子の
運動を厳密に計算できるタイプの作用素となります。その作用素を組み
合わせた作用素もまた粒子の運動を厳密に計算できるものになるのです。
先の2つの作用素を (p(0),q(0)) に作用させて得られる
(p(Δt),q(Δt))は
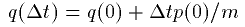 (13)
(13)
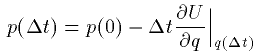 (14)
(14)
となります。これを1次のSymplectic解法と呼びます。
あまりEuler法とかわりないように思われるでしょうが
実は大きな違いがあるのです。
第4章 非可換微分作用素の指数法則
目次
Copyright(C) by Naoki Watanabe. Oct 21st, 1995.
渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp