第2章 微分作用素による運動方程式の記述
1粒子の運動をHamilton形式で見ることから始めましょう。
粒子の位置を q 、運動量を p とし、この粒子の
Hamitonianを H とします。
運動方程式は以下のようになります。
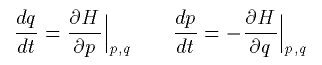 (01)
(01)
ここで (p,q) をベクトルとして見てみましょう。
すると、このベクトルの時間変化は、Hamitonianの形と、
そのベクトル自身によって決まることになります。
つまりベクトルに対して、Hamitonianから決まる特殊な作用を施すと、
その時間変化のベクトルになると見ることができます。
その作用素を D と表すことにしましょう。
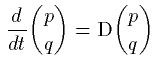 (02)
(02)
このように書くと D が行列の様ですが、行列はなく、
ベクトルからその時間変化を表すベクトルに変換する作用素です。
この作用素は時刻tによって変化しません。
Hのみによってきまるのです。
ところで、普通のスカラー量のx,kに対しての微分方程式とその解
 (03)
(03)
と(02)式の作用素の方程式とを比較するとその解は
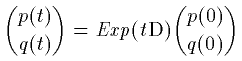 (04)
(04)
となるような気がしませんか?
ここで、作用素の指数が登場しましたが、これの意味は次の通りです。
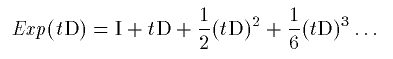 (05)
(05)
つまり exp のテイラー展開のそのままです。
テイラー展開ですので、t があまり大きいと具合がわるいので、
以後は有限の短い時間 Δt に置き換えます。
D を (p,q) に作用させると、(02)式より
その1階微分が求まります。
D を (p,q) に2回作用させると、
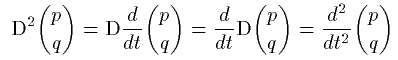 (06)
(06)
となるので2階微分が求まります。
よって D を n 回作用させると (p,q) の
n 階微分が求まることになります。
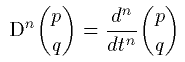 (07)
(07)
ここで(04)式にこの指数関数の定義式を代入し、作用の処理を施すと
次の結果になります。
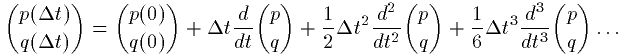 (08)
(08)
これは (p(Δt),q(Δt)) の (p(0),q(0))
まわりのテイラー展開になるではないですか。
よって(04)式には正当性があるのです。
第3章 微分作用素の分割
目次
Copyright(C) by Naoki Watanabe. Oct 21st, 1995.
渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp
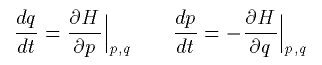 (01)
(01)