第5章 影のHamiltonian
Symplectic法の作り方と使い方はわかりましたが、この方法が
なぜそれほど注目されているかがまるでわかりません。Symplectic
Integratorの最大の特徴のエネルギー保存について解説します。
作用素を無限積で表示して、それを有限積で近似しました。このときの
近似で数値積分に誤差が起こります。しかし、その誤差の振る舞に、
とてつもない性質があるのです。
指数関数の有限積は、一つの指数関数に必ずまとめらることが
知られています。すなわち、
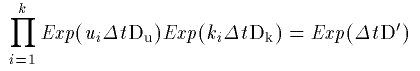 (26)
(26)
この D' はもちろん D とは違います。その違いは、
u_i,k_i を求めるときに無視した Δt^nのオーダーです。
さらにこのD' に対して、これを生成するハミルトニアンH'
が存在します。
有限積による積分では、この影のハミルトニアン H' の系での
粒子の運動を完全に予測するものなのです。エネルギーもこの系では厳密に
保存されます。
H' の H との差は Δt^n のオーダーなので、
H'から解かれた(p,q)でHの値を求めると、
振動はするものの、その振幅はΔt^nのオーダーであって
決してエネルギーの単調増大減少は起こり得ないのです。
これがSymplectic数値積分法がエネルギーを保存する原理です。
近似度を高めることは、エネルギーの振動の振幅を小さくするためなのです。
第6章 指数作用素のフラクタル分割(前編)
目次
Copyright(C) by Naoki Watanabe. Oct 21st, 1995.
渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp
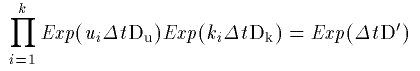 (26)
(26)