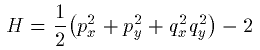 (00)
(00)Euler法やRunge-Kutta法などの差分法は、ある物理量の現在の時間微分 から未来を予測する方法で数値積分を行なっていました。しかし、この方法 では原理的に誤差が生じ、それが蓄積され、系のエネルギーの発散などの 実際にはあり得ない結果となります。
Δt を小さくすると、その誤差は少なくなりますが、逆に計算回数が 増えるので、かけ算などでの計算誤差が入ってきてしまいます。
数値積分ではこの誤差は仕方のないことだと思われがちなのですが、 この問題を解決する新しい数値積分法が1980年代の終りごろから登場 しました。その名も Symplectic Integrator(シンプレクティック数値積分法)です。 そして 1990年代前半に鈴木増雄先生(現 東京大学名誉教授) によって演算子の指数の指数積展開の理論として体系化されました。
この数値積分法はいままでの差分法とは全く異なる理論により作られて います。その詳細は以降の章で解説することにして、その結果は 系のエネルギーを原理的に保存する数値積分法となるのです。 しかも使い方がEulerによく似ていて誰でも簡単に利用できるのです。
この数値積分法の利用分野は古典力学系に限らず量子多体系、乱流解析 にも利用可能と言われています。まさに次世代のコンピュータ物理学を 支える重要な理論かつ技術なのです。
この数値積分法がどのくらい凄いものなのかをお見せしましょう。 例として、鈴木増雄先生が論文で使われたHamiltonianを用います。 そのHamiltonianは、
と与えられます。初期値としてこの系のエネルギーは理論的には初期値
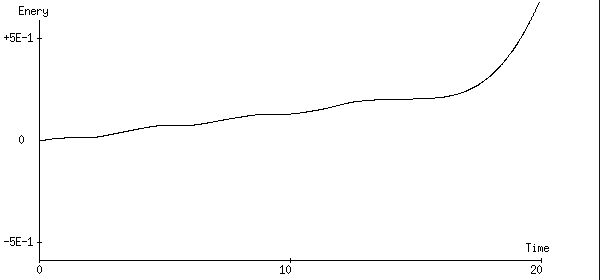
1次Euler法:あっというまにエネルギーは発散してしまいt=20までしか
表示できませんでした。もし発散しなければt=2000までの計算に
かかる時間は40秒です。
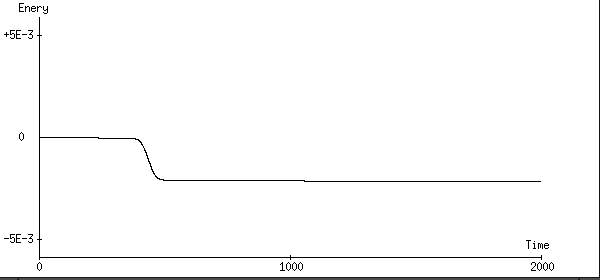
4次Runge-Kutta法:t=300付近から段階的にエネルギーが減少しています。
エネルギーの発散が起こらないだけEuler法よりはましでしょう。
計算にかかった時間は300秒です。時間がかかります。
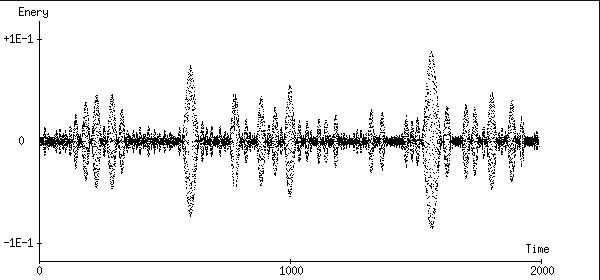
1次Symplectic法:エネルギーが奇妙な振舞いをしています。
いたる所々で非常に激しい振動が起こっています。まるで
カオスの分岐図がフラクタルの様にならんでいる様です。
振動の後にはエネルギーは元の値に戻ります。
計算にかかった時間は40秒です。1次Euler法と同程度です。
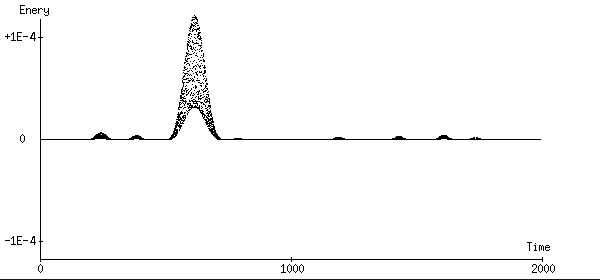
4次Symplectic法:エネルギーが上向きのみに所々で振動しています。
振動の振幅は1次Symplectic法のものより1000分の1程度に小さくなって
います。これも振動の後にはエネルギーは元の値に戻ります。
計算にかかった時間は130秒です。1次Symplectic法の約3倍です。
このようにSymplectic法はエネルギーが振動するにもかかわらず また元のエネルギーに落ち着くという性質がある数値積分法なのです。 また計算時間がそれほどかからないことも長所です。 このエネルギーの振動は次数を上げることで劇的に小さくすることが できるのです。
Symplectic法のすばらしさがおわかりいただけたことでしょう。 ではその詳細な解説を次章から始めます。