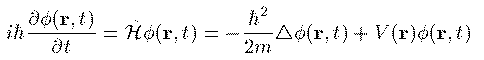 (01)
(01)本節では波動関数の時間発展を計算してみよう。
計算対象の系として、1次元波束がpotential障壁
によって散乱される様子と井戸型potential内の電子が外部電磁波により
励起される様子を計算しよう。
Schrodinger方程式の波動関数の定常解を求める作業が難しい
固有値問題であるのと異なり、波動関数の時間発展を求める作業は
簡単な時間積分の問題である。しかしながらこの時間積分の計算にも大事な
技術や方法論がいくつかある。本節ではこれらの技術も学ぼう。
位置 r 、時刻 t での波動関数の値 φ(r,t) を 方程式から直接計算するのが実空間での計算である。 これに対して、 φ(r,t) の fourier展開係数 φ(k,t) の従う 方程式から φ(k,t) を計算して、逆fourier変換で φ(r,t) を計算するのが波数空間での計算である。 実空間での計算の方が実用化が簡単なのでまずこの計算法を解説する。
Hamiltonian が H で記述される系の波動関数 φ(r,t) は 次のSchrodinger方程式に従って時間発展する。
(1)式は形式的に厳密に解くことができる。 初期値 φ(r,0) に対する時刻 Δt での 形式解 φ(r,Δt) は次式で与えられる。 この U を時間推進演算子と呼ぶ。波動関数の確率密度の全空間での積分値、つまり粒子の存在確率に 注目しよう。時刻 Δt での存在確率は(2)式に より時刻 0 での存在確率と次のように関係付けられる。
最後の等式ではHamitonianがHermite演算子であることを用いた。 結局、存在確率は保存される。これは物理的に最も基本的な 要請でもある。この要請は時間推進演算子 U の unitarity U^†U = 1 によって満たされるのである。時間微分を時間間隔 Δt で差分化しよう。 形式的厳密解 (2)式を Δt の1次まで展開した 次の差分化が最も簡単である。
時刻 Δt での値が時刻 0 での値から直接的に求まる 陽的差分スキームである。しかし unitarity は満たされていない。 存在確率は保存されずに単調増加するので、 (5)式の差分化はこの問題の解法には不適切である。(2)式の U は unitary であり、その逆演算子が U^† であることを利用すると次の差分化ができる。
左辺の値が右辺の値と等しくなるように φ(r,Δt) を 調整することなる。この式を形式的に次式で表す。 時刻 Δt での値が時刻 0 での値から間接的に求まる 陰的差分スキームである。しかし unitarity は満たされていない。 存在確率は保存されずに単調減少するので、 (7)式の差分化もこの問題の解法には不適切である。Unitarity を満たすもっとも簡単な近似は (5)式と(8)式 を合わせた次式である。
つまり陽的に半ステップ Δt/2 進み、陰的に半ステップ Δt/2 進む のである。時間差分は2次精度となっている。この形式をCayley形式と呼ぶ。 U の unitarity が厳密に満たされていることは容易に確かめられる。 存在確率は厳密に保存され、さらに保存すべき物理量はすべて厳密に 保存される。このため(10)式の差分化はこの問題の 解法に適切なのである。Cayley形式を具体的な形に変形しよう。 この式から、Cayley形式(10)式での計算は 時間変化分の計算に時刻 0 と時刻 Δt の平均値を使うことと等価で あることがわかる。陽的と陰的を半々に合わせた(12)式 の差分スキームを一般にCrank-Nicholsonの差分スキームと呼ぶ。空間を1次元とし、(1)式を原子単位系 hbar=1,m=1,e=1 で再び書き下す。
空間も間隔 Δx で離散化しよう。離散化した空間のindexを i 、時刻の indexを n として、その位置時刻の波動関数を φ_i^n で表す。 空間の2階偏微分を2次精度の中心差分で差分化することにして (13)式を(11)式のCayleyの 形式で差分化すると次式となる。 この式から φ_i^{n+1} を求めるにはまず、各 i について (15)式の右辺を計算する。その結果を変数 b_i^n に格納する。つまり、 次に(15)式の左辺の連立方程式を解く。 この連立方程式は非常に特殊な形をしているので、この解法作業は 比較的軽い作業で済む。解法の理論は数値計算の本を参考のこと。 本書ではこの特殊な型の連立方程式を解く関数 TriDiagEQ( Complex A[], Complex x[], Complex b[] ) を提供して、これをブラックボックスとして使うことにする。 興味のある読者はこの関数の中身をよく調べてみると良い。これで波動関数の時間発展を実空間で精度良く解く方法が確立した。
| 物理量 | 1単位の量 | SI単位系での値 |
| 作用 | hbar | 1.054572666e-34 [Js] |
| 質量 | m | 9.109389754e-31 [kg] |
| 電荷 | e | 1.602177335e-19 [C] |
| エネルギー | mc^2α^2 | 4.359748230e-18 [J] |
| 運動量 | mcα | 1.992853378e-24 [kgm/s] |
| 長さ | \hbar/mcα | 5.291772479e-11 [m] |
| 時間 | \hbar/mc^2α^2 | 2.418884326e-17 [s] |
量子力学のトンネル効果により、粒子は薄いpotential障壁を
通り抜けることができる。波動関数の時間発展を計算してこの様子を
観察しよう。また粒子が反射する様子にも興味深い現象がある。
計算をするためには系の大きさを有限にしなくてはならない。
系を長さ L の1次元系とする。系の両端に無限大の potentialを仮定して、
両端での波動関数の値を 0 に固定する。系の中央には矩形のpotential障壁を
設置する。
運動する粒子の波動関数は次式で定義される
Gaussian波束で表現することができる。
プログラムを設計し始めよう。ソースファイル名は scatt.cc である。 まずは諸定数の定義である。
空間に割り当てる格子点の数を GRIDS に指定する。 空間の分割数は GRIDS-1 になることに注意しよう。 系の大きさは原子間隔程度を想定してボーア半径の 8倍、 電子の運動エネルギーは 288\Unit{a.u} 、 Potential障壁の高さは電子のエネルギーの少し高めの1.25倍にした。#include "cip.h" #include "nxgraph.h" #include "complex.h" //---- experimental settings const double dT = 1.0/4096; // temporal step const int GRIDS = 256+1; // number of GRIDS points //---- physical settings // settings about the system const double SYS_LEN = 8.0; // length of the system const double dX = SYS_LEN/(GRIDS-1); // length of a cell, dont edit // settings about initial conditions of the Gaussian wave packet const double PAC_POS = 2.0; // initial position const double PAC_DX = 1.0/4; // initial width const double PAC_MOM = 24.0; // initial momentum const double PAC_ENE = sqr(PAC_MOM)/2; // kinetic energy, dont edit // settings about the potential barrier const double BAR_POS = 4.0; // position const double BAR_LEN = 1.0/8; // length const double BAR_HIG = PAC_ENE*1.25; // height or barrier energy //---- graphics settings const int WIN_WIDTH = 512; const int WIN_HEIGHT = 256; const int BASE_Y = 228; // Y-coordinate of the origin const double WAVE_MAG = 64.0; // magnify factor for wave const double POTE_MAG = 1.0/4; // magnify factor for potential
プログラムの基幹である波動関数を管理する機構を作るのが簡潔であろう。 その class Wave を宣言する。
//---- declaration of class Wave
class Wave
{
Complex phi[GRIDS];
public:
Wave( void );
void Evolve( void );
void Draw( void );
private:
void TriDiagEQ( Complex A[], Complex x[], Complex b[] );
double Probability( void );
double Energy( void );
};
これらのmethodを定義する前に、 Wave classのobjectと相互作用 するpotentialを管理するclass Potential を宣言する。
//---- declaration of class Potential
class Potential
{
double V[GRIDS];
public:
Potential( void );
inline double operator [] ( int i ){ return( V[i] ); }
void Draw( void );
};
次に Wave classのmethodを定義する。Constructorでは (18)式に従ってGaussian波束を波動関数に設定する。
//---- sets Gaussian wave packet
Wave::Wave( void )
{
const double Amp = pow( 2*M_PI*sqr(PAC_DX), -0.25 );
for( int i=1 ; i<=GRIDS-1 ; i++ ){
double x = dX*i;
phi[i] = Amp * exp( -sqr((x-PAC_POS)/(2*PAC_DX)) ) * expCI( PAC_MOM*x );
}
phi[0] = phi[GRIDS-1] = 0.0;
}
時間発展を計算する Evolve() methodとその下請けの TriDiagEQ() methodを定義する。
//---- evolves the wave function by using Cayley's form
void Wave::Evolve( void )
{
extern Potential V; // assumes the existence of an object V
static Complex b[GRIDS], A[GRIDS], B[GRIDS];
for( int i=1 ; i<=GRIDS-2 ; i++ ){
B[i] = CI*4*dX*dX/dT + (2 + V[i]*2*dX*dX)*C1;
A[i] = CI*4*dX*dX/dT - (2 + V[i]*2*dX*dX)*C1;
b[i] = B[i]*phi[i] - phi[i+1] - phi[i-1];
}
TriDiagEQ( A, phi, b );
}
//---- soleves equations of special tri-diagonal matrix
void Wave::TriDiagEQ( Complex A[], Complex x[], Complex b[] )
{
static Complex u[GRIDS];
int i;
u[1] = 1.0/A[1];
x[1] = b[1]*u[1];
for( i=2 ; i<=GRIDS-2 ; i++ ){
u[i] = 1.0/(A[i]-u[i-1]);
x[i] = (b[i]-x[i-1])*u[i];
}
for( i=GRIDS-3 ; i>=1 ; i-- ){
x[i] -= x[i+1]*u[i];
}
}
TriDiagEQ() methodは対角要素が A[] で上下の複対角要素が 1 である特殊な3重対角行列をLU分解して、その解を高速に計算する。 詳しくは数値計算の本を参照のこと。Indexの走る範囲が 1 から GRIDS-2 までである理由は、系の両端の波動関数の値を 0 に固定した ため、時間発展を計算する必要が無いからである。
粒子の存在確率とエネルギー期待値を計算するmethodを定義する。
//---- calculates integral of probability density
double Wave::Probability( void )
{
double prob=0.0;
for( int i=0 ; i<GRIDS ; i++ ){
prob += abs2(phi[i])*dX;
}
return( prob );
}
//---- calculates expectational energy
double Wave::Energy( void )
{
extern Potential V;
double energy=0.0;
for( int i=1 ; i<GRIDS-1 ; i++ ){
energy += Real( conj(phi[i]) *( (2*phi[i] - phi[i+1] - phi[i-1])/(2*dX*dX) + V[i]*phi[i] ) ) * dX;
}
return( energy );
}
//---- draws wave function
void Wave::Draw( void )
{
int i;
// draws probability density
NXSetColor( NX_BLUE );
NXDrawMoveto();
for( i=0 ; i<GRIDS ; i++ ){
NXDrawLineto( int(i*dX*WIN_WIDTH/SYS_LEN),
BASE_Y - int(abs2(phi[i])*WAVE_MAG) );
}
// prints some values
NXSetColor( NX_BLACK );
NXDrawPrintf( 16, WIN_HEIGHT-16, "Probability = %lf", Probability() );
NXDrawPrintf( 16, WIN_HEIGHT-2, "Energy = %lf", Energy() );
}
//---- sets potential
Potential::Potential( void )
{
for( int i=0 ; i<GRIDS ; i++ ){
if( BAR_POS - BAR_LEN/2 < dX*i && dX*i < BAR_POS + BAR_LEN/2 ){
V[i] = BAR_HIG;
}else{
V[i] = 0.0;
}
}
}
//---- draws potential
void Potential::Draw( void )
{
NXSetColor( NX_GREEN );
NXDrawMoveto();
for( int i=0 ; i<GRIDS ; i++ ){
NXDrawLineto( int(i*dX*WIN_WIDTH/SYS_LEN),
BASE_Y - int(V[i]*POTE_MAG) );
}
}
最後に Wave classと Potential classのobjectを global変数として定義して main() 関数でプログラムを 統括する。
//---- definition of fundermental objects
Potential V;
Wave W;
//---- Main function
int main( void )
{
XEvent ev;
NXOpenWindow( "Scattering", WIN_WIDTH, WIN_HEIGHT );
NXEnable( NX_DOUBLEBUFFER );
do{
for( int i=0 ; i<16 ; i++ ){
W.Evolve();
}
NXClearWindow();
W.Draw();
V.Draw();
NXFlush();
}while( NXCheckEvent( NX_NOWAIT, ev ) != KeyPress );
NXCloseWindow();
return(0);
}
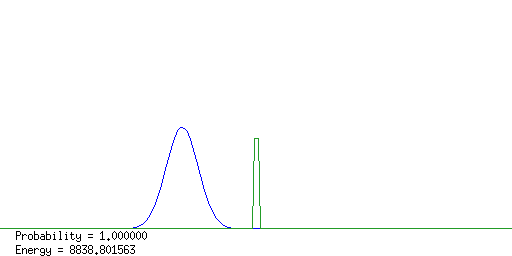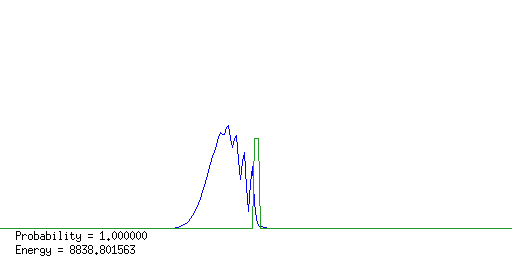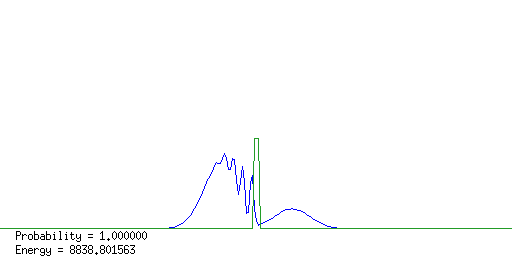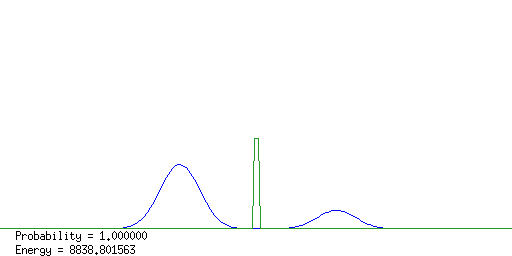
計算結果のアニメーションのいくつかのコマを右に載せる。 入射波束がpotential障壁によって散乱され、透過波束と反射波束に わかれる様子がよくわかる。
散乱完了直後に障壁右側の粒子の存在確率を計算すると 粒子の透過確率がわかる。障壁の高さ、長さ、電子のエネルギー、 透過確率との間の関係を各自調べてみよ。 また、入射波束と反射波束の中心位置の 時間変化を測ると、粒子が障壁に衝突して直ちに反射しているのでは ないことがわかる。この時間のずれと障壁の関係に付いて考察してみよ。
 |
波動関数が少数の基底関数の線形結合で表されることがわかっている場合 には、波動関数を実空間で差分化して計算するよりも基底関数の結合係数 を計算する方が遥かに計算コストが少なく精度も良い。
有界な任意の関数はFourier級数で表すことができるので、 Hamiltonianに無関係で境界条件を満たす基底関数の線形結合で 任意の波動関数を完全に表すことができる。普通この基底関数系には 簡単に計算できる非摂動系の定常状態の固有波動関数系を用いることが多い。
時間に依存する相互作用のある系のHamiltonian H(r,t) を時間に依存せず固有波動関数が簡単に求まる部分 H^0(r) と それ以外の部分 H'(r,t) にわけよう。 H^0(r) の系の固有波動関数 φ_n(r) は次の時間に依存しない Schrodinger方程式を満たす。
そして H(r,t) の系の波動関数 Ψ(r,t) は次の時間に依存する Schrodinger方程式に従う。 Ψ(r,t) を φ_n(r) で展開する。 (21)式を(20)式に代入して (19)式を使い、さらに φ_n の規格直交性を用いると 展開係数の運動方程式が得られる。 実空間の計算量が格子点の数に比例するのに対して、 波数空間の計算量は基底関数の数の2乗に比例する。 しかしその比例係数は後者の方が遥かに小さい。このため少数の基底関数で 展開できる場合は波数空間での計算が有理である。1次元井戸内の基底状態にある電子が振動数 ω の電磁波を受けて 遷移する過程を追ってみよう。井戸の長さを L とする。固有波動関数系 ψ_n(x) とエネルギー E^0_n は次の通りである。
電子は量子力学的に扱うが、電磁波は古典的外場として扱う半古典的な 手法をとろう。電磁波と電子の相互作用 H' は複雑だが、 第1次近似として、電気双極子近似と呼ばれる簡単な相互作用 H_ED で近似できる。 電場の振動方向を x 軸に合わせた。 E_{rm amp} は電場の振幅である。 (26)式の相互作用は一様電場のpotentialに他ならない。 磁場の効果や電場が波として変動している効果は微小な2次近似でしかない。プログラムを設計し始めよう。ソースファイル名は rabi.cc である。 まずは諸定数の定義である。
#include "cip.h"
#include "nxgraph.h"
#include "complex.h"
//---- experimental settings
const double dT = 1.0/2048; // temporal step
const int BASES = 4; // number of base waves
//---- physical settings
// setting about the well
const double WEL_LEN = 1.0; // length of the well
// setting about the wave function
const int WAVE_MODE = 0; // initial mode
// inline macros for eigen_values
inline double eigen_moment( int mode ){
return( M_PI/WEL_LEN*(mode+1) );
}
inline double eigen_energy( int mode ){
return( 0.5*sqr(M_PI/WEL_LEN*(mode+1)) );
}
// setting about the electromagnetic-wave
const double Eamp = 4.0; // amplitude of elecro-wave
const double Omg = eigen_energy( WAVE_MODE+1 ) - eigen_energy( WAVE_MODE ); // angular frequency
//---- graphics settings
const int WIN_WIDTH = 512;
const int WIN_HEIGHT = 256;
const int BASE_Y = 128; // Y-coordinate of the origin
const double WAVE_MAG = 64.0; // magnify factor for wave
const double POTE_MAG = 16.0; // magnify factor for potential
const int GRIDS = 64+1; // number of GRIDS for drawing
波動関数を管理するclass Wave を宣言する。内容は 実空間のものとはかなり異なる。
//---- declaration of class Wave
class Wave
{
// property of each base functions
Complex C[BASES]; // coefficiences
double E0[BASES], k0[BASES]; // eigen energy and momentum
double d[BASES][BASES]; // matrix elements of dipole
public:
Wave( void );
void Evolve( void );
void Draw( void );
private:
double Probability( void );
Complex Phi( double x );
};
電磁波を管理するclass EleMag を宣言する。 しかし単に振動電場の値を計算保持するだけである。 内容が簡単なmethodはここで定義しよう。
//---- declaration of class EleMag
class EleMag
{
double Ele; // Electro-field
public:
EleMag( void ){ Ele = 0.0; }
inline double E( void ){ return( Ele ); }
void Evolve( void );
void Draw( void );
};
次に Wave classのmethodを定義する。 Constructorでは理論式に従ってpropertyを設定する。
//---- initializes properties
Wave::Wave( void )
{
int n, m;
for( n=0 ; n<BASES ; n++ ){
if( n == WAVE_MODE ) C[n] = 1.0; else C[n] = 0.0;
k0[n] = eigen_moment(n);
E0[n] = eigen_energy(n);
for( m=0 ; m<BASES ; m++ ){
if( (n-m)%2 != 0 ){
d[n][m] = (8.0*WEL_LEN/(M_PI*M_PI)) * ((double)(n+1)*(m+1)/sqr(sqr(n+1)-sqr(m+1)));
}else{
d[n][m] = 0.0;
}
}
}
}
電子系の時間発展のmethod Evolve() を 定義する。(23)式の数値積分にはSymplectic 数値積分法を用いよう。
//---- evolves the wave function
void Wave::Evolve( void )
{
extern double T; // assumes the existence of an object T
extern EleMag F; // assumes the existence of an object F
double D = F.E(); // gets the electric field
int n, m;
// symplectic integration part I.
for( m=0 ; m<BASES ; m++ ){
for( n=0 ; n<BASES ; n++ ){
if( (n-m)%2 == 0 ) continue;
C[n] += -(dT/2)*D*d[n][m]*CI*C[m];
}
}
// symplectic integration part II.
for( n=0 ; n<BASES ; n++ ){
C[n] = expCI(-dT*E0[n])*C[n];
}
// symplectic integration part III.
for( m=BASES-1 ; m>=0 ; m-- ){
for( n=0 ; n<BASES ; n++ ){
if( (n-m)%2 == 0 ) continue;
C[n] += -(dT/2)*D*d[n][m]*CI*C[m];
}
}
}
double Wave:::Probability( void )
{
double prob=0.0;
for( int n=0; n<BASES ; n++ ){
prob += abs2(C[n]);
}
return( prob );
}
そして波動関数を描くmethod Draw() を定義する。 しかし波数空間で計算したため実空間での値に戻す作業が必要である。
//---- invert sin transform
Complex Wave::Phi( double x )
{
extern double T;
Complex phi=0.0;
for( int n=0; n<BASES ; n++ ){
phi += C[n] * sin(k0[n]*x);
}
return( phi );
}
//---- draws wave function
void Wave::Draw( void )
{
int i;
static Complex phi[GRIDS];
const double dX = WEL_LEN/(GRIDS-1); // length of a cell
// converts into real space
for( i=0 ; i<GRIDS ; i++ ){
phi[i] = Phi(dX*i);
}
// draws probability density
NXSetColor( NX_BLUE );
NXDrawMoveto();
for( i=0 ; i<GRIDS ; i++ ){
NXDrawLineto( int(i*dX*WIN_WIDTH/WEL_LEN),
BASE_Y - int(abs2(phi[i])*WAVE_MAG) );
}
// draws real part of the wave function
NXSetColor( NX_CYAN );
NXDrawMoveto();
for( i=0 ; i<GRIDS ; i++ ){
NXDrawLineto( int(i*dX*WIN_WIDTH/WEL_LEN),
BASE_Y - int(Real(phi[i])*WAVE_MAG) );
}
// draws imaginaly part of the wave function
NXSetColor( NX_GRASS );
NXDrawMoveto();
for( i=0 ; i<GRIDS ; i++ ){
NXDrawLineto( int(i*dX*WIN_WIDTH/WEL_LEN),
BASE_Y - int(Imag(phi[i])*WAVE_MAG) );
}
// draws coefficiences as rectangle bars
NXSetColor( NX_BLACK );
for( int n=0 ; n<BASES ; n++ ){
int h = int(128*abs2(C[n]));
NXFillRectangle( n*32+16, WIN_HEIGHT-1-h, 24, +h );
}
// prints some values
NXDrawPrintf( 16, 16, "Probability = %lf", Probability() );
}
次に EleMag classのmethodの定義である。
//---- updates electro-field
void EleMag::Evolve( void )
{
extern double T;
Ele = Eamp*sin(Omg*T);
}
//---- draws electro-field
void EleMag::Draw( void )
{
NXSetColor( NX_BLACK );
NXDrawLine( int(0*WIN_WIDTH/WEL_LEN),
BASE_Y - int(Ele*0*POTE_MAG),
int(WEL_LEN*WIN_WIDTH/WEL_LEN),
BASE_Y - int(Ele*WEL_LEN*POTE_MAG) );
}
最後に Wave classと EleMag class のobjectと時間の変数 T を global変数として定義して main() 関数でプログラムを統括する。
//---- definition of fundermental objects
double T = 0.0;
Wave W;
EleMag F;
int main( void )
{
XEvent ev;
NXOpenWindow( "Rabi oscillation", WIN_WIDTH, WIN_HEIGHT );
NXEnable( NX_DOUBLEBUFFER );
do{
for( int i=0 ; i<16 ; i++ ){
F.Evolve();
W.Evolve();
T += dT;
}
NXClearWindow();
F.Draw();
W.Draw();
NXFlush();
}while( NXCheckEvent( NX_NOWAIT, ev ) != KeyPress );
NXCloseWindow();
return(0);
}
計算結果のアニメーションを下に載せる。 青線の曲線は井戸内の電子の確率密度、黄緑と水色の曲線は波動関数の 実部と虚部、黒色の直線は電場によるポテンシャル、左下の棒グラフは 各準位の占有率を表す。
基底波動関数が徐々に第1励起状態の波動関数に変化していく様子が わかる。さらに上への励起は起こらず再び基底状態に戻る。 これは誘導放出で光子が放出されるためである。 電子の存在確率は基底と励起状態の間を振動することがわかる。 このような振動をRabi振動と呼ぶ。
この計算では光の振動数を電子系の遷移エネルギーに合わせたのでその 間の遷移しか観測されないが、光の振動数や振幅を変えるとどうなるかを 調べてみよ。振幅をかなり大きくすると興味深い現象が起こる。
振動電場に合わせて電子の存在位置も振動しているが、これは分極が 生じていることを示す。電場の振幅をかなり大きくすると、この分極が作る 局所的な電場の振舞いに重大な変化が現れる。その様子を調べてみよ。
ところで、励起状態には寿命があるので電磁波が無くても自然放出で光子 が放出されるはずである。時間発展の方程式 (23)式では その効果を考慮していないが簡単に拡張することができる。弱い光では、 電子は励起しても自然放出で落ちるのでRabi振動は観測されない。 Rabi振動は強いレーザー光で観測されるのである。

|