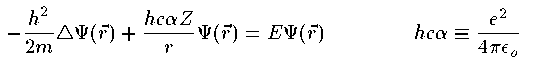
量子力学の発端となった水素ガスの輝線の系列の謎の法則には、 1913年にM.Bohrによってある程度理論的な説明が与えられたが、 物理学者たちは古典力学の限界を強く感じていた。 この難問に解決の糸口を与え、新たな物理学を創造した巨匠が W.HeisenbergとE.Schrodingerであることはあまりにも有名である。
Schrodingerは1926年に自身の提案したSchrodinger方程式を用いて 水素原子のエネルギー準位を見事に説明した。彼は数学の遺産である特殊関数 を駆使してこれを導いたのだが、現在の我々は計算機という強力な道具で Schrodinger方程式を解くことができる。いささか人間が退化したかの ように聞こえるかもしれないが、計算機を用いて問題を解くことには プログラムを学ぶこと以外にもそれなりの苦労が必要である。また 計算機を用いればもっと複雑な問題を解決することができ、過去の巨匠たち が想像すらできなかった新たな物理について知ることができるのである。
前置きが長くなったが、この節と続く何節かで原子中の電子の波動関数と エネルギー準位を計算する方法を学ぼう。 まず本節で1次元問題として Schrodinger 方程式から水素原子の1個の 電子の波動関数の動径部分とエネルギーを求める。次の節で 相対論的量子力学のDirac方程式を用いて同じ問題を解く。さらに次の 節で波動関数の球面部分を求めて3次元に広がる電子軌道の絵を描く。 そして最後の節で多電子原子の全電子の波動関数とエネルギーを求める ことにしよう。
原子番号 Z の原子核のCoulomb potential での Schrodinger 方程式は以下の通りである。
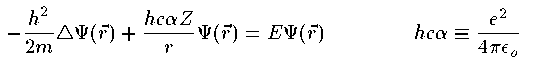
原子核のCoulomb potentialのみの系の動径波動関数には解析解がある。 これは計算機による数値解の信頼性を確認する上で重要である。 信頼性を確認したら、解析解のないより複雑な系へと進むことができる。
原子核のCoulomb potential中での動径波動関数 R_{nl}(r) に r をかけた関数 G_{nl}(r) の解析解は次の通りである。
ここで L_{n+l}^{2l+1} は Laguerre陪多項式であり である。いくつかの G_{nl}(r) を以下に載せる。 ここで大事な法則が2つある。potentialの種類に依らず、束縛状態の 動径波動関数 G_{nl}(r) は原点と無限遠において値が 0 である。 これは電子の確率密度の全空間での積分が有限であることに起因する。 またこれらの箇所以外にも n-l-1 箇所で値が 0 になる節(node)を 持つ。これは波動関数の直交性に起因する。 前者の法則は波動関数の境界条件に使われ、後者の法則は波動関数が 指定した量子数のものかを判定するのに使われる。束縛状態の波動関数には境界条件が課さられエネルギーは離散的な準位しか 許されない。逆に、境界条件を満たす波動関数となるようなエネルギーを 探せばそれがエネルギー準位に他ならないのである。 これが計算機で Schrodinger 方程式を解く基本戦略である。 エネルギー E の初期暫定値を仮定して、以下の作業を繰り返す。

動径波動関数を求める作業の概略図
微分方程式から G,F を解き進むためには、端点での値、すなわち 境界条件を与える必要がある。用いる解法の都合上、端点のみでなく 端点周辺の4点での G,F の値が必要になっている。 端点近傍であることを利用して(2)式を 簡単な形に近似して解析解を筆算で求めて、端点近傍の値を計算する。 potentialが原点近傍で 1/r^2 より緩やかならば、 原点近傍の G,F の規格化されていない近似解は次の通りである。
potentialが遠方で十分小さければ、 遠方での G,F の近似解は次の通りである。 かなり大雑把な近似解であるが、端の条件としてはこれで十分である。水素原子の問題から離れて一般論として 微分方程式の数値解法のひとつであるHamming法を紹介する。
x の未知関数 y(x) の微係数が y'=f(x,y) と 与えられているとする。 4つの格子点での y の値 y_{i-1}, y_{i-2}, y_{i-3}, y_{i-4} が 既に求まっている時に、次の格子点での値 y_i をHamming法は 次の手順で計算する。
内側、外側の両方からHamming法で G,F を 接続点 r_{fit} まで計算し、接続点での両者の G の値が 連続するように外側の G,F を定数倍する。エネルギーが正しくなければ G のrによる1階微分値 G'=F/r は連続しない。 仮に接続点にデルタ関数型のpotential Cδ(r-r_{fit}) がそこにあれば、1階微分値の屈折が起こる。これを逆に利用して G' も連続させるエネルギーの修正分を見積る。 簡単な計算によりデルタ関数の因子 C は次のように表される。
このデルタ関数のpotentialを摂動として、1次の摂動エネルギー E^1 は となる。ただし G は規格化されているとした。この E^1 が G の1階微分を不連続にさせている余分なエネルギーに他ならない。 E から E^1 を引いたより正しいエネルギーを用いて、波動関数を最初から 計算しなおす。プログラムを設計する準備が整った。ソースファイルは radschro.cc である。 まずは諸定数の定義である。
R_NUM が動径方向の格子点数である。この再遠方の格子点を簡潔に 表せるように R_FAR を用意しておく。 DX は x 座標系での セルの大きさ、 R_O はBohr半径に相当する所の格子点のindexである。 波動関数を出力する際には OUTPUT_R_MAX で定める距離より 遠くは除くことにする。#include "cip.h" //---- physical settings const double Z = 1.0; //---- experimental settings const double DX = 0.0625; // size of a cell in x-space const int R_NUM = 256; // total number of grids const int R_FAR = R_NUM-1; // index of farthest grid const int R_O = 160; // index of Bohr radius const double OUTPUT_R_MAX = 64.0; // max radius output [a.u]
中心から各格子点までの距離をテーブルにしておこう。 Z によるスケール変換も考慮しておく。
//---- table of Radius
class RTable
{
double r[R_NUM];
public:
RTable( void ){
for( int i=0 ; i<=R_FAR ; i++ ){
r[i] = (1.0/Z)*exp(DX*(i-R_O));
}
}
inline double operator [] ( int i ){
return( r[i] );
}
} R;
Potentialを管理するclassを用意しよう。ただし管理する物理量は potential V(r) に中心からの距離を掛けた量 U(r)=rV(r) である。 原子核のCoulomb potentialだけなら、 U=-Z であり、わざわざ classを用意するまでもないが、他のpotentialへの応用に備えてこの class Potential にまとめておこう。
class Potential
{
double U[R_NUM]; // rV, potential muliplied by radius
public:
Potential( void ){
for( int i=0 ; i<=R_FAR ; i++ ){
U[i] = -Z; // Coulomb potential of nuclear
}
}
double operator [] ( int i ){ return( U[i] ); }
};
プログラムの主題である動径波動関数を管理計算するclass Orbital を設計する。宣言部分は次のようになる。
class Orbital
{
int n, l; // quantum numbers
double E; // energy of this orbital
double G[R_NUM], F[R_NUM]; // wave function
public:
void Assign( int _n, int _l );
void Adjust( void );
void Output( void );
private:
inline double CalcDG( int i, double P[], double G, double F );
inline double CalcDF( int i, double P[], double G, double F );
int PreInteg( double P[] );
int HammingA( double P[], int i_fit );
int HammingB( double P[], int i_fit );
void Normalize( double a, int i_fit );
};
まず Assign() method で軌道の量子数を設定する。 ついでに軌道エネルギーの見積りを与えておく。 この見積りには正解からわずかにずれた値を与えておこう。
//-- sets quantum numbers
void Orbital::Assign( int _n, int _l )
{
n = _n; l = _l;
E = -0.5*Z*Z/(n*n)-0.01; // a guess of the true energy
}
動径波動関数の計算の指揮をとる method Adjust() である。 エネルギー固有値と固有波動関数を捜し当てる。
//-- calculates radial wave function
void Orbital::Adjust( void )
{
static double P[R_NUM];
double GA, GB, LogA, LogB, dE;
int true_node = n-l-1, node, i_fit;
do{
i_fit = PreInteg( P ); // prepares integration
node = HammingA( P, i_fit ); // integrates from origin
GA = G[i_fit]; // stores G at the fitting grid
LogA = F[i_fit]/(R[i_fit]*G[i_fit]); // stores logarithmic derivative of G at the fitting grid
node += HammingB( P, i_fit ); // integrates from far
GB = G[i_fit]; // stores G at the fitting grid
LogB = F[i_fit]/(R[i_fit]*G[i_fit]); // stores logarithmic derivative of G at the fitting grid
Normalize( GA/GB, i_fit ); // connects and normalize
dE = -0.5*sqr(G[i_fit])*(LogB-LogA); // estimates energy modification
if( node != true_node ){ // if node is violated
dE = double(true_node-node)/(n*n*n); // rough modification
}else if( fabs(dE) > 1.0e-2 ){ // if still large error
dE *= 0.5; // smaller modification
}
E+=dE; // modifies energy
if( E>0.0 ){ // it can't be binding state
fprintf( stderr, "Energy can not converge.\n" );
exit(1);
}
}while( fabs(dE)>1e-8 ); // repeats until the modification is sufficiently small
fprintf( stderr, "Orbital energy of (%d %d) has converged to %16lf [a.u]\n", n, l, E );
}
ループ冒頭の PreInteg() methodは以後の積分計算に必要な 諸量を計算する。適合点のindexを戻り値とする。 HammingA() 、 HammingB() methodはそれぞれ内側外側から 波動関数を積分して構築する。計算結果の節の数と適合点の両側での G の値とその対数微分を記録しておく。 Normalize() methodは両側の波動関数を連結して全体を規格化する。 そして (21)式に従ってエネルギーの必要な修正分を 見積もる。 波動関数の節の数が真の数と異なる程エネルギーが大きくずれている 場合には修正分を大雑把なものにする。また一次摂動による修正分が やや大きい場合にはそれをそのまま使うと修正しすぎることがあるので 修正分を半分に変更する。束縛状態を求めているのでエネルギーが 0 を 越えるはずはないので、この場合、エネルギーの見積りがあまりに不適切 だったとして計算を中止する。 このような計算をエネルギー修正分が十分小さくなるまで繰り返す。 ここで登場した下請けmethod たちを設計していこう。
PreInteg() methodは G[],F[] の x による微係数を計算するのに 必要な係数の配列 P[] を(3)(4)式に 従って設定する。この時、potentialについての情報が必要になるので Potential classの object U を extern 宣言しておく。 さらに両端周辺の4点での G[],F[] の値を (14)(15)式に従って設定する。 そして接続点に適当なindexを P[] から判断して戻り値とする。
//---- prepares for integration
int Orbital::PreInteg( double P[] )
{
extern Potential U;
int i;
for( i=0 ; i<=R_FAR ; i++ ){ // sets parameters for differential equation
P[i] = 2*R[i]*U[i] - 2*sqr(R[i])*E + l*(l+1);
}
for( i=0 ; i<4 ; i++ ){ // sets G,F at near origin
G[i] = pow(R[i],l+1); F[i] = (l+1)*G[i];
}
double a = -sqrt(-2*E); // sets G,F at far away
for( i=R_FAR ; i>R_FAR-4 ; i-- ){
G[i] = exp(a*R[i]); F[i] = (a*R[i])*G[i];
}
for( i=R_FAR ; P[i]>0.0 && i>=0 ; i-- ); // searches the cross grid and reports it as the fitting grid
return( i );
}
次に G[],F[] の各点での微係数を計算する補助methodを 設計しよう。ここで先に計算した配列 P[] が使われる。
//---- represents derivative of G
inline double Orbital::CalcDG( int i, double P[], double G, double F ){
return( F );
}
//---- represents derivative of F
inline double Orbital::CalcDF( int i, double P[], double G, double F ){
return( P[i]*G + F );
}
この微係数を計算するmethodを使って、 HammingA() methodは内側から G[],F[] を積分し、 HammingB() methodは外側から G[],F[] を積分する。 i_fit が両者の適合点のindexである。 両者ともその間にある G[] の節の数を報告する、
//---- integrates from origin to the fitting grid
int Orbital::HammingA( double P[], int i_fit )
{
int i, node=0;
double Gp, Fp, Gm, Fm, Gc, Fc, Gpc=0.0, Fpc=0.0, dGm, dFm;
static double dG[R_NUM], dF[R_NUM];
for( i=0 ; i<4 ; i++ ){ // prepares derivatives at grids near origin
dG[i] = CalcDG( i, P, G[i], F[i] );
dF[i] = CalcDF( i, P, G[i], F[i] );
}
for( ; i<=i_fit ; i++ ){ // integrates from the origin to the fitting grid
Gp = G[i-4] + (4.0*DX/3.0)*( 2*dG[i-1] - dG[i-2] + 2*dG[i-3] ); // calculates predictors
Fp = F[i-4] + (4.0*DX/3.0)*( 2*dF[i-1] - dF[i-2] + 2*dF[i-3] );
Gm = Gp - (112.0/121.0)*( Gpc ); // calculates modifiers
Fm = Fp - (112.0/121.0)*( Fpc );
dGm = CalcDG( i, P, Gm, Fm ); // calculates derivative at modifiers
dFm = CalcDF( i, P, Gm, Fm );
Gc = (9.0/8.0)*(G[i-1]) - (1.0/8.0)*(G[i-3]) // calculates correctors
+ (3.0*DX/8.0)*(dGm + 2*dG[i-1] - dG[i-2]);
Fc = (9.0/8.0)*(F[i-1]) - (1.0/8.0)*(F[i-3])
+ (3.0*DX/8.0)*(dFm + 2*dF[i-1] - dF[i-2]);
Gpc = Gp - Gc; // calculates difference between predictors and correctors
Fpc = Fp - Fc;
G[i] = Gc + (9.0/121.0)*Gpc; // calculates the next step
F[i] = Fc + (9.0/121.0)*Fpc;
dG[i] = CalcDG( i, P, G[i], F[i] ); // calculates derivative at the next step
dF[i] = CalcDF( i, P, G[i], F[i] );
if( G[i]*G[i-1] < 0 ) node++;
}
return( node );
}
//---- integrates from far to the fitting grid
int Orbital::HammingB( double P[], int i_fit )
{
int i, node=0;
double Gp, Fp, Gm, Fm, Gc, Fc, Gpc=0.0, Fpc=0.0, dGm, dFm;
static double dG[R_NUM], dF[R_NUM];
for( i=R_FAR ; i>R_FAR-4 ; i-- ){ // prepares derivatives at far grids
dG[i] = CalcDG( i, P, G[i], F[i] );
dF[i] = CalcDF( i, P, G[i], F[i] );
}
for( ; i>=i_fit ; i-- ){ // integrates from far to the fitting grid
Gp = G[i+4] - (4.0*DX/3.0)*( 2*dG[i+1] - dG[i+2] + 2*dG[i+3] ); // calculates predictors
Fp = F[i+4] - (4.0*DX/3.0)*( 2*dF[i+1] - dF[i+2] + 2*dF[i+3] );
Gm = Gp - (112.0/121.0)*( Gpc ); // calculates modifiers
Fm = Fp - (112.0/121.0)*( Fpc );
dGm = CalcDG( i, P, Gm, Fm ); // calculates derivative at modifiers
dFm = CalcDF( i, P, Gm, Fm );
Gc = (9.0/8.0)*(G[i+1]) - (1.0/8.0)*(G[i+3]) // calculates correctors
- (3.0*DX/8.0)*(dGm + 2*dG[i+1] - dG[i+2]);
Fc = (9.0/8.0)*(F[i+1]) - (1.0/8.0)*(F[i+3])
- (3.0*DX/8.0)*(dFm + 2*dF[i+1] - dF[i+2]);
Gpc = Gp - Gc; // calculates difference between predictors and correctors
Fpc = Fp - Fc;
G[i] = Gc + (9.0/121.0)*Gpc; // calculates the next step
F[i] = Fc + (9.0/121.0)*Fpc;
dG[i] = CalcDG( i, P, G[i], F[i] ); // calculates derivative at the next step
dF[i] = CalcDF( i, P, G[i], F[i] );
if( G[i]*G[i+1] < 0 ) node++;
}
return( node );
}
Normalize() methodは両領域の波動関数を連結しさらに規格化する。 引数 a には外側領域にかけるべき因子を与える。
//---- normalizes wave function
void Orbital::Normalize( double a, int i_fit )
{
int i;
double sum, norm;
for( i=i_fit ; i<=R_FAR ; i++ ){
G[i] *= a; F[i] *= a;
}
for( i=0, sum=0.0 ; i<=R_FAR ; i++ ){
sum += sqr(G[i])*R[i]*DX;
}
for( i=0, norm=sqrt(1.0/sum) ; i<=R_FAR ; i++ ){
G[i] *= norm; F[i] *= norm;
}
}
//---- outputs wave function
void Orbital::Output( void )
{
for( int i=0 ; i<=R_FAR ; i++ ){
printf("%lf %lf\n", R[i], G[i] );
if( R[i]>OUTPUT_R_MAX ) break;
}
printf("\n");
}
//---- definition of fundermental objects
static Potential U;
static Orbital O;
//---- main function
int main( void )
{
for( int n=1 ; n<=3 ; n++ ){
for( int l=0 ; l<n ; l++ ){
O.Assign( n, l );
O.Adjust();
O.Output();
}
}
return(0);
}
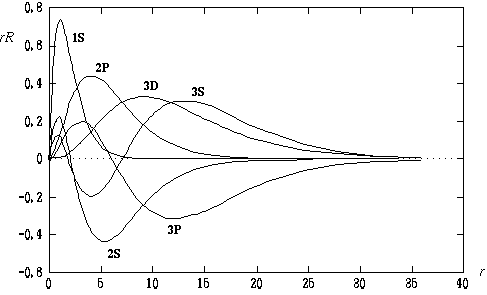
このプログラムが計算した種々の動径波動関数