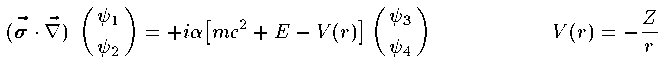 (1)
(1)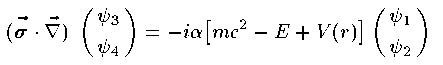 (2)
(2)Dirac方程式は量子力学を特殊相対論のLorentz変換に対して共変な形式に するために、Schrodinger方程式にかわる基本方程式として1928年に P.Diracによって導入された方程式である。Dirac方程式はLorentz不変で あるだけではなく、スピンの概念を元から備え、スピン軌道相互作用に よる準位の分裂を自然に正しく導くのである。
Dirac方程式はSchrodinger方程式より複雑だが、その解法はかなり 似ている。本節では前節で設計したSchrodinger版のプログラムを 改造してDirac版のプログラムにしよう。
Dirac方程式は4つの成分を持った波動関数(Dirac spinor)に対する 4元1階の連立微分方程式である。 波動関数を Ψ=(ψ_1,ψ_2,ψ_3,ψ_4) とすると 定常状態の Dirac方程式は次の通りである。
ここで σ は3つのPauli行列をまとめたベクトルである。波動関数の個々の成分 ψ_i もまた動径部分と球面部分に分解すること ができ、その解はやや複雑な計算により導かれる。結果だけを紹介する。
波動関数は4つの量子数 (n,l,j,m) でラベルされる。
スピン平行な場合 (j=l+1/2)
スピン反平行な場合 (j=l-1/2)
2つの動径波動関数 G_{nj}^{l}(r),F_{nj}^{l}(r) の 従う方程式は次の通りである。
ここで k はスピン平行の場合 k=-l-1 、スピン反平行の場合 k=l を表す。Schrodingerの時と同様に座標系を r=e^x として変換する。
これがDirac方程式での解くべき方程式である。 Schrodinger 方程式でのものと形式的には大差がないことがわかる。Coulomb potentialで基底状態 (n=0,l=0,j=1/2) の動径波動関数の解析解を紹介する。
ここで γ=√{1-α^2} である。 各軌道のエネルギー準位は次の通りである。Coulomb potentialでの原点近傍での G,F の近似解は次の通りである。
遠方での G,F の近似解は次の通りである。2つの動径波動関数 G,F を接続点で滑らかに連続させるようにエネルギー を修正する。 G'/G が接続点で連続ならば自動的に F'/F も連続 になる。従って G だけに注目すればよい。 前節と同様にデルタ関数の摂動potential Cδ(r-r_{jnt}) を 考えてエネルギーの修正分を見積る。その結果 次の様になる。
ただし G^2+F^2 が規格化されているとした。プログラムの基本骨子はSchrodinger版と同じである。これを 何箇所か改造することでDirac版ができあがる。 ソースファイルはraddirac.ccである。 根本的な改造箇所のみを載せていく。
原子単位系で電子の静止質量エネルギーを表す定数 MC2 を定義する。
const double MC2 = 1.0/(ALPHA*ALPHA); // mass energy of eletron [a.u]
Orbital class の property に量子数を表す int k と double j が加わる。 k の値は Assign() methodで次のように設定する。エネルギーの見積もりは 質量エネルギーも含めて次のようになる。
//-- sets quantum numbers
void Orbital::Assign( int _n, int _l, double _j )
{
n = _n; l = _l; j = _j;
if( j-l==0.5 ) k = -l-1; else k = l;
E = MC2/sqrt(1+sqr(ALPHA/(n-(j+0.5)+sqrt(sqr(j+0.5)-ALPHA*ALPHA)))) - 0.001; // a guess of the true energy
}
LogA = F[i_fit]/G[i_fit];
LogB = F[i_fit]/G[i_fit];
dE = -MC2*ALPHA*(sqr(G[i_fit])+sqr(F[i_fit]))*(LogB-LogA);
//---- represents derivative of G
inline double Orbital::CalcDG( int i, double P[], double G, double F ){
return( P[i+R_NUM]*F - k*G );
}
//---- represent derivative of F
inline double Orbital::CalcDF( int i, double P[], double G, double F ){
return( P[i]*G + k*F );
}
//---- prepares for integration
int Orbital::PreInteg( double P[] )
{
extern Potential U;
int i;
for( i=0 ; i<=R_FAR ; i++ ){ // set parameters for differential equation
P[i] = ALPHA*(MC2-E)*R[i] + ALPHA*U[i];
P[i+R_NUM] = ALPHA*(MC2+E)*R[i] - ALPHA*U[i];
}
double a, f; // set G,F at near origin
a = sqrt(k*k-ALPHA*ALPHA);
f = (1.0/ALPHA)*(k+a);
for( i=0 ; i<4 ; i++ ){
G[i] = exp( a*log(R[i]) );
F[i] = f*G[i];
}
// set G,F at far away
a = -ALPHA*sqrt( MC2*MC2-E*E );
f = -sqrt((MC2-E)/(MC2+E));
for( i=R_FAR ; i>R_FAR-4 ; i-- ){
G[i] = exp(a*R[i]);
F[i] = f*G[i];
}
// searches the cross grid and reports it as the fitting grid
for( i=R_FAR ; P[i]>0.0 && i>=0 ; i-- );
return( i );
}
for( i=0 ; i<=R_FAR ; i++ ){
sum += sqr(G[i])*R[i]*DX;
sum += sqr(F[i])*R[i]*DX;
}
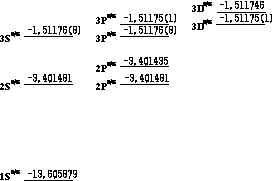
このプログラムが計算したDirac方程式による
水素原子のエネルギー準位の概略図
エネルギーの基準は無限遠方、単位は[eV]、()は誤差
このプログラムが出力する動径波動関数 G の姿はSchrodinger方程式 でのものと見掛け上ほとんど差が無いが、エネルギーに重大な違いが 表れる。Schrodinger方程式で縮退していた幾つかの準位に 分裂が起こるのである。これは電子のスピンと軌道との相互作用の大きさの 違いによる現象であり、Dirac方程式によって定性的に説明される 現象である。上図にいくつかの準位を表す。ただし準位の分裂幅は 非常に狭いので図ではそれを誇張している。
Dirac方程式は量子論を相対論的に拡張する優れた方程式であるが完璧な論理 ではない。具体的な欠陥は実はすでにこれまでの式に出てきている。 水素原子には問題は無いが、原子番号 Z の重い原子核ではその 微細構造定数 α は水素のそれの Z 倍となる。従って Z > 137 の非常に重い原子核がもし作られたら、その α は 1 を越える。 この時、式(12)式中の a ≡√{k^2-α^2} の値は、 k^2=1 に対して純虚数となる。 こうなると波動関数は原子核近傍で振動してしまい、Kleinのparadoxと 呼ばれるさまざまな矛盾が発生する。特に反粒子と呼ばれる本来負の エネルギーを持つ粒子のエネルギー準位が正のエネルギーを持つ粒子の エネルギー準位と区別ができなくなり、そのため、電子-陽電子対が無限 に生成されるという非常事態となる。
この問題はQED(量子電磁力学)やQCD(量子色力学)にも残り、 反応のmatrix elementを α の1次か2次のTaylor展開で 計算している議論は、 α > 1 の状態ではそのすべてが破綻する。 QCDの諸量を近似展開せずに計算するにはファイマン経路積分を計算するの だが、この計算を直接行うことはほぼ不可能である。そこで格子ゲージ理論 により、経路積分を空間格子点で波動関数が独立の値を取る格子模型の 分配関数の計算にすり替える。 格子の問題になれば、それはモンテカルロ法により計算することが 可能になる。ただし、計算量は超膨大であり、スーパーコンピュータを 長時間かけて計算することになる。 現在、この手法により、いままで未解決だった問題に 計算機による答えが与えられようとしている。