Quantum:Orbital of Hydrogen Atom

● 水素原子の電子軌道のorbital

動径波動関数に続いて球面波動関数を計算して、電子軌道のorbitalを電子雲として描いてみよう。

■ 球面波動関数

▲ 球面調和関数

ポテンシャルが中心力ならば、ポテンシャルの形や基本とする方程式にかかわらず球面波動関数は球面調和関数 Y_l^m である。この関数は解析的に完全に知られているのでそれを借用することにする。

(1)

N_{lm} は規格化定数である。

(2)

P_l^m(z) は Legendre陪関数(associated Legendre polynomial)であり、Legendre関数 P_l(z) と共に次式で定められる。

(3)

P_l^m(z) を計算が行えるように多項式で表すと次式になる。

(4)

このままでは扱いにくいので次のように整理する。

(5)
(6)

m+l が偶数の場合 i=2j
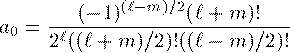(7)

m+l が奇数の場合 i=2j+1
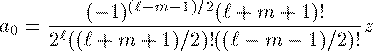(8)

この計算は桁落ち誤差を招きやすいので本当はよろしくないが、小さい l,m に対してはなんとか使える。そして Φ_m(φ) は

(9)

である。これで球面波動関数を計算できるようになった。参考のためいくつかの軌道の Y_l^m(θ,φ) を載せておく。

(10)
(11)
(12)
(13)
(14)
(15)

▲ 波動関数の実数化

波動関数の φ 部分 Φ_m(φ) は e^{imφ} の複素数である。そこでよく使われる方法はこれと縮退している Φ_{-m}(φ) の波動関数と足し引きして sin(mφ) と cos(mφ) の2つの実数関数を作ることである。Dirac spinorの場合でも同様にスピンと軌道の磁気量子数を反対にしたものとで実数関数を作ることができる。もちろん磁場か何かの影響で縮退が解けたらこの方法は使えない。 Φ_m(φ) 単独での分布は 1 なので z 軸に対称となる。

■ 分布関数を乱数で表現する方法

電子雲を描くためには電子の分布関数を乱数で表現する方法を理解しておかなければならない。この方法は後に紹介するモンテカルロ法で絶対的に重要な事項であるので、その初歩的なことだけをここで学んでおこう。

▲ 逆変換法

粒子の位置を一回だけ測定して、区間 [x,x+dx] 内に観測する確率 f(x)dx は波動関数 φ(x) を用いて、

(16)

と表されることは周知であろう。ここで登場した f(x) は分布関数と呼ばれる。測定を何度も繰り返すことでこの分布関数 f(x) の姿が見えてくる。

この様子をコンピュータでシミュレーションすることを考えてみよう。つまり粒子を観測する位置を分布関数 f(x) に従う乱数 x で決定するのである。その様な乱数を生成するための最も単純な方法が逆変換法である。

分布関数 f(x) に従って乱数 x が生成できたとする。 f(x) の定義域下限 x_{min} から x までの範囲の f(x) の面積 S(x) すなわち積算分布関数の値は区間 [0,1] を一様に分布することに注目しよう。つまり区間 [0,1] を一様に分布する乱数を r と表せば

(17)

の関係なのである。この関係を逆に用いれば、一様乱数 r から分布関数 f(x) に従う乱数 x が生成されるのである。これが逆変換法である。 f(x) の数式が知られている場合には

(18)

を筆算で計算しておもむろに乱数 x を生成することができる。しかし、 S^{-1}(r) が解析的に求まらない場合が往々にしてある。そのような場合の対処法は電磁シャワーの節で紹介する。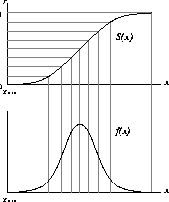

他方、 f(x) が数値的にしか知られていない場合には、数値積分で積算分布関数 S(x) を求めておいて、乱数 r から適切な S(x) を与える x を探すことにより乱数 x を生成することになる。

プログラムでの実装の例を示そう。分布関数を n 点の配列 f[] に格納しておく。積算分布関数を配列S[] に設定する関数 Accumulate() と S[] を元に分布に従うindexを返す関数 Sample() は安直には次のようになる。

void Accumulate( int n, double f[], double S[] )
{
  int i;
  double sum, norm;

  for( i=0, sum=0.0 ; i<n ; i++ ) S[i] = (sum+=f[i]);             // accumulate area
  for( i=0, norm=1.0/sum ; i<n ; i++ ) S[i] *= norm;              // normalize area
}

int Sample( int n, double S[] )
{
  int i;
  double r = Urand();

  for( i=0 ; i<n ; i++ ) if( S[i] > r ) break;
  return( i );
}

S[] の規格化も行うように設計したので、f[] が規格化されていなくてもよい。この仕組みは球面波動関数の計算において多くの計算を省略する。

▲ 電子の位置のサンプルの取り方

3次元の分布関数 f(r) が各次元の分布関数の直積で表される場合、つまり

(19)

この場合、3次元の位置のサンプルを得るには単に各次元ごとに独立してサンプルを求めるだけである。

Dirac spinor Ψ=(ψ_1(r),ψ_2(r),ψ_3(r),ψ_4(r)) での分布関数 f(r) は各成分の絶対値の2乗の和である。

(20)

各成分が各次元の分布関数の積なので全体の分布関数 f(r) は各次元の分布関数の直積ではない。この場合、全空間での各成分の占有率に応じて乱数で成分のひとつを選び、その成分について3次元独立にサンプルを得ればよい。

■ プログラムの実装

Orbitalを描くための準備がこれですべて整った。計算結果はXlibを用いてwindowに絵を描くことにしよう。 3次元の絵なので回転するアニメーションが楽しい。ソースファイルは orbital.ccである。まずは諸定数の定義と関数プロトタイプの宣言からである。

#include "cip.h"
#include "nxgraph.h"

//---- definition of fundermental constants
//---- experimental settings
const int    R_NUM        = 256;           // total number of cell
const int    TH_NUM       = 128;           // number of polar cell
const double dTH          = M_PI/TH_NUM;   // step of polar angle
const int    PH_NUM       = 128;           // number of azimuthal cell
const double dPH          = 2*M_PI/PH_NUM; // step of azimuthal angle

//---- graphics settings
const int    PLOT_NUM     = 2048;
const int    WIN_HEIGHT   = 512;
const int    WIN_WIDTH    = 512;
const double MAG          = 16.0;

//---- prototypes of functions
void CalcRadial( int n, int l, double Frad[] );
void CalcPolar( int l, int m, double Fthe[] );
void CalcAzimuthal( int m, double Fphi[] );
void Accumulate( int n, double f[], double S[] );
int  Sample( int n, double S[] );
void DetectOrbital( short x[], short y[], short z[], double Srad[], double Sthe[], double Sphi[] );
void DrawOrbital( double the, short x[], short y[], short z[] );

PLOT_NUM は電子を測定する回数であり多いほど雲が濃くなり orbitalがはっきり見える。しかしもちろんあまり多すぎると計算や描画が大変になり、アニメーションも見苦しいものとなってしまう。

main() 関数の説明に入ろう。分布関数と積算分布関数を格納するための配列群を定義する。

//---- main function
int main( void )
{
  int    n, l, m;
  double Frad[R_NUM], Fthe[TH_NUM], Fphi[PH_NUM]; // distribution
  double Srad[R_NUM], Sthe[TH_NUM], Sphi[PH_NUM]; // accumulated distribution
  short  x[PLOT_NUM], y[PLOT_NUM], z[PLOT_NUM];   // observed coordinates
  XEvent ev;
  NXOpenWindow("Orbital of Hydrogen Atom", WIN_WIDTH, WIN_HEIGHT );
  NXEnable( NX_DOUBLEBUFFER );

  for( l=0 ; ; l++ ){
    n = l+1; // no meaning
    for( m=+l ; m>=-l ; m-- ){
      printf("(n,l,m)=(% d,% d,% d)\n", n, l, m );
          // calculate radial distribution and its accumulated one
      CalcRadial( n, l, Frad );
      Accumulate( R_NUM,  Frad,  Srad );
          // calculate polar distribution and its accumulated one
      CalcPolar( l, m, Fthe ); 
      Accumulate( TH_NUM, Fthe, Sthe );
          // calculate azimuthal distribution and its accumulated one
      CalcAzimuthal( m, Fphi );
      Accumulate( PH_NUM, Fphi, Sphi );
          // observe electron PLOT_NUM times and store their coordinates
      Observe( x, y, z, Srad, Sthe, Sphi );
          // draw rotating orbital
      for( double the=0.0 ; the < 2*M_PI ; the+=0.0625 ){
        Draw( the, x, y, z );
        NXCheckEvent( NX_NOWAIT, ev );       // recieve keyboard hit
        if( ev.type == KeyPress ){
          if( ev.xkey.keycode == 'q' ) goto LOOPOUT;
          if( ev.xkey.keycode == 'n' ) break;
        }
      }
    }
  }
 LOOPOUT:;
  NXCloseWindow();

  return(0);
}

作業の手順は容易にわかるであろう。このプログラムは各orbitalを 1回転して次のorbitalに移るが nキーが押されると直ちに次の軌道に移り、 qキーでプログラムを終了するようにしてある。

続いて r 方向の分布関数を計算するCalcRadial() である。動径波動関数は 2P軌道のもののみを使っているが、前節までの動径波動関数を求めるプログラムとあわせるなり、他の軌道の解析解を計算するなり各自で改良してほしい。

//---- calculate distribution of radial wave function
void CalcRadial( int n, int l, double Frad[] )
{
  for( int i=0 ; i<R_NUM ; i++ ){
    double r = R[i];
    Frad[i] = sqr(r*r*exp(-r));    // only 2p orbital!
  }
}

θ方向の分布関数を計算するCalcPolar() 関数は Legendreの陪関数を簡単化したものを漸化式で計算する。

//---- calculate distribution of polar wave function
void CalcPolar( int l, int m, double Fthe[] )
{
  int    i, it;
  double z, z2, a, s;

  m = abs(m);
  for( it=0 ; it<TH_NUM ; it++ ){
    z  = cos(dTH*it);
    z2 = z*z;
    if( (l+m)%2 ){      // odd
      i = 3;    a = z;
    }else{              // even
      i = 2;    a = 1;
    }
    for( s=a ; i<=l-m ; s+=a, i+=2 ){
      a *= z2*(i-l+m-2)*(i+l+m-1)/(i*(i-1));
    }
    Fthe[it] = sin(dTH*it) * pow( 1-z2, m ) * s*s;
  }
}

φ 方向の分布関数を計算するCalcAzimuthal() 関数は m>0 では -m の波動関数と足して cos 型にしたもの設定し、 m<0 では -m の波動関数と引いて sin 型にしたもの設定する。

//---- calculate distribution of azimuthal wave function
void CalcAzimuthal( int m, double Fphi[] )
{
  for( int i=0 ; i<PH_NUM ; i++ ){
    if( m == 0 )     Fphi[i] = 1;
    else if( m > 0 ) Fphi[i] = sqr(cos(m*dPH*i));
    else if( m < 0 ) Fphi[i] = sqr(sin(m*dPH*i));
  }
}

そして積算分布関数から電子の位置のサンプルを大量に得る Observe() 関数である。

//---- observe electron many times
void Observe( short x[], short y[], short z[], double Srad[], double Sthe[], double Sphi[]  )
{
  for( int i=0 ; i<PLOT_NUM ; i++ ){
    double rad = R[ Sample( R_NUM, Srad  )];
    double the = dTH*Sample( TH_NUM, Sthe );
    double phi = dPH*Sample( PH_NUM, Sphi );
    
    x[i] = short(MAG*rad*sin(the)*cos(phi));
    y[i] = short(MAG*rad*sin(the)*sin(phi));
    z[i] = short(MAG*rad*cos(the)         );
  }
}

最後にorbitalの絵をアニメーションとして描くDraw() 関数である。外部変数 CV,CS は座標回転の行列要素である。

//---- rotation matrix
static double CV, SV;

//---- transform real coordinates into window coordinates
inline int Wx( short x, short y, short z ){
  return( (WIN_WIDTH/2) + int(CV*x-SV*y) );
}
inline int Wy( short x, short y, short z ){
  return( (WIN_HEIGHT/2) - int(z) + int((1.0/4)*(SV*x+CV*y)) );
}

//---- draw orbital
void Draw( double the, short x[], short y[], short z[] )
{
  CV = cos(the);    SV = sin(the);
  NXClearWindow();
  for( int i=0 ; i<PLOT_NUM ; i++ ){
    NXDrawPoint( Wx(x[i],y[i],z[i]), Wy(x[i],y[i],z[i]) );
  }

  const int AXIS = WIN_WIDTH/2;
  NXDrawLine( Wx(-AXIS,0,0), Wy(-AXIS,0,0), Wx(+AXIS,0,0), Wy(+AXIS,0,0) );  // X-axis
  NXDrawLine( Wx(0,-AXIS,0), Wy(0,-AXIS,0), Wx(0,+AXIS,0), Wy(0,+AXIS,0) );  // Y-axis
  NXDrawLine( Wx(0,0,-AXIS), Wy(0,0,-AXIS), Wx(0,0,+AXIS), Wy(0,0,+AXIS) );  // Z-axis
  NXFlush();
}

以下にこのプログラムが描く電子雲のいくつかを載せる。プログラムはこれをアニメーションとして回転するので、 orbitalの様子がよくわかる。量子力学の確率解釈についての理解が深まるであろう。

1s (1 0 0)	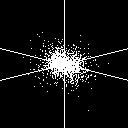2p_x (2 1 +/-1)	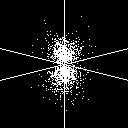2p_z (2 1 0)	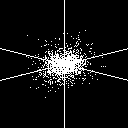2p_y (2 1 -/+1)

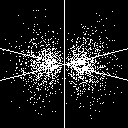3d_{x^2-y^2} (3 2 +/-2)	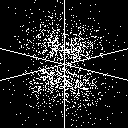3d_{zx} (3 2 +/-1)	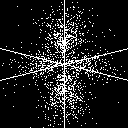3d_{z^2} (3 2 0)	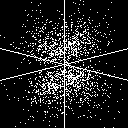3d_{yz} (3 2 -/+1)	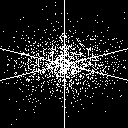3d_{xy} (3 2 -/+2)

このプログラムが描く種々の電子軌道

渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp