 (1)
(1)水素原子の1つの電子の波動関数が計算できたので、 複数の電子を持つ多電子原子の各電子の波動関数を求めよう。 電子間のCoulomb相互作用のため、方程式を代数的に解くことは 不可能であり、まさにコンピュータに頼るところである。
N 電子系の波動関数 Ψ とそれを支配する方程式の 導出の導出の過程を歴史にそって簡単に紹介しよう。
1928年に D.R.Hartree は電子 i が位置 r_1 で感じる他の電子の potential Vh_i(r_1) を次の平均値で扱うことを提案した。
φ_j は電子 j の軌道波動関数、 ρ_{except-i}(r_2) は電子 i 以外の全電子の電荷密度、 そして r_{12} は r_1 r_2 間の距離である。この Vh_i(r_1) が求まれば、残りの問題は電子 i の軌道波動関数 φ_i(r_1) の1電子方程式の問題となる。Hartree方程式
が支配方程式となる。この方程式の固有値 E_i と固有関数 φ_i を 軌道の準位や縮重度に応じて選択することにより各電子の軌道波動関数と エネルギーが求まる。ただし E_i は イオン化エネルギーであって1電子のエネルギーではない。 Hartree はこの方程式を直観的に提案したが、J.C.Slaterは N 電子系の 波動関数 Ψ を次の各電子の軌道波動関数 φ_i(r_i) の 直積で表現し、Schrodinger方程式で全エネルギーを求め、それを 最小にする変分問題としてHartree方程式を導出した。 こうして、多電子系の波動関数を1電子ごとに分けて1電子方程式 にすることにより、解くべき問題が明確になった。Hartree方程式では「電子 i 」として電子の個性を認めていた。 しかしPauliの原理によりこれは認められない。さらに N 電子系の波動関数 Ψ は各電子のスピン軌道座標 ξ_i について 反対称化されていなくてはならない。Slaterはこの原理を満たす N 電子系の波動関数 Ψ を次のような 各電子のスピン軌道波動関数 Ψ_i(ξ_i) の行列式で表現した。
世に名高いSlater行列式である。FockはSchrodinger方程式で この波動関数の全エネルギーを求め、それを 最小にする変分問題として以下の Hartree-Fock方程式を導いた。 この方程式は各電子の軌道波動関数 φ_i についての方程式である。Vh(r_1) は電子間のCoulomb相互作用を表し、その内容は次の 通りである。
Vh_i(r_1) と似ているが、電荷密度は全電子の電荷密度であり、 どの電子の方程式についても共通であることが異なる。Vx(r_1) は交換相互作用を表す演算子であり軌道波動関数 φ_i に対して 次のように作用する。
電子 i のスピンが上向きの場合
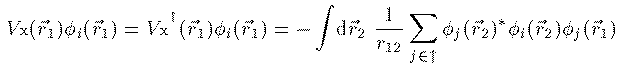 (7)
(7)
電子 i のスピンが下向きの場合
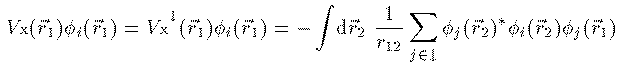 (8)
(8)
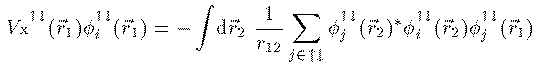 (9)
複矢印同順ということである。
(9)
複矢印同順ということである。
このHartree-Fock方程式によりPauli原理の要請を満たす軌道波動関数と エネルギーが求まる。
Hartree-Fock 方程式の Vx の演算子の作用の計算はその定義式を見ての 通り複雑である。1951年、Slaterは自由電子ガスを想定してこの項の計算を 劇的に簡単にする近似式を導き、さらにその方法を束縛系であるこの 多電子原子系にも応用することを提案した。この方法はその単純化の割には 良好な計算結果を出してくれる。
Slaterによると Vx^{↑↓}(r_1) は次のように Vsl^{↑↓}(r_1) で近似される。
これをHartree-Fock方程式に適応した式を Hartree-Fock-Slater方程式あるいは単にSlater近似と呼ぶ。1964年、P.Hohenberg とW.Kohn は電子系の基底エネルギーが 電子密度 ρ(r) の汎関数として表されることを証明し、 翌年、W.Kohn と L.J.Sham はこれを次のように表した。
このエネルギーを最小にする条件を変分計算で求めることにより 次の Kohn-Sham 方程式が得られる。 Vxc は交換相関相互作用と呼ばれ、これの厳密な表式を求める 研究が現在も続いている。この項が厳密に求まれば、多電子系の 方程式は近似無しの厳密な形として得られることになる。 本書では1971年にL.HedinとB.I.Lundqvistが量子モンテカルロ法によって 求めた次の交換相関相互作用を用いる。ここで r_s(r_1) はWigner半径と呼ばれ、電子1つがそこで占める球の 半径を表す。
原子系のエネルギーを波動関数ではなく電子密度の汎関数で表すことから 出発するこの方法は密度汎関数法(density functional theory)と呼ばれる。 さらに交換相関を上記のように局所的な電子密度で近似したものは 局所密度近似(Local Density Approximation(LDA))、総じて 局所密度汎関数法と呼ばれる。この種の計算方法は原子だけでなく、 分子、結晶、表面などの電子状態の計算にも使われ、 計算物質科学(Computational Material Science)の分野での 第一原理計算(First Principal Calculation)による研究の 基本手法となっている。
プログラムに取りかかる前にまだ幾つか紙の上で処理しておくことがある。
方程式(14)式での 固有値 E_i は軌道エネルギーと呼ばれるエネルギーの次元を持った 量であるが、これは電子 i のエネルギーでもイオン化エネルギーでもない。 従って軌道エネルギーの 総和は N 電子系の全エネルギーではない。 全エネルギーは N 電子系の波動関数 Ψ を Schrodinger方程式に入れ直して求める。その結果、 全エネルギー E は次式で表される。
電子 iのイオン化エネルギー I_i は、その電子の軌道の占有数 n_i が
n_i=0 である系と n_i=1 である系の全エネルギーの差
I_i = E_{n_i=0} - E_{n_i=1} のことである。
Koopmansの定理によると、その2つの系で
他の電子の状態が同じであると仮定すれば、
Hartree-Fock方程式の軌道エネルギー E_i を使って
I_i = - E_i と表すことができる。 ところが、Slater近似以降の方程式では軌道エネルギー E_i は
次式が示すように、その軌道の占有数 n_i を連続量として
全エネルギーを偏微分して n_i=1 としたものになっている。 このことを利用して、イオン化エネルギー I_i は次のように表される。
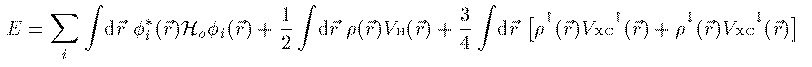 (15)
(15)
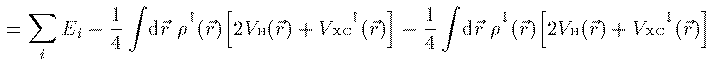 (16)
(16)
▲ イオン化エネルギー
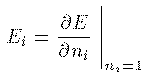 (17)
(17)
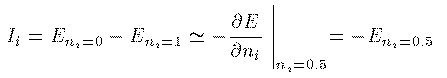 (18)
(18)
全電子の電荷密度 ρ(r) は一般に角度に依存する。そのため個々の電子 の波動関数を動径部分と球面部分の直積に分解することはできない。しかし、 分解できなければ計算が困難になる。なので思い切って全電子の電荷密度が 角度に依存しないと仮定しよう。この仮定により各電子の波動関数の 球面部分は水素原子同様に球面調和関数で表され、動径部分 R_i(r_i) に r_i をかけた量 G_i(r_i) の満たすべき方程式は次のようになる。
基礎方程式
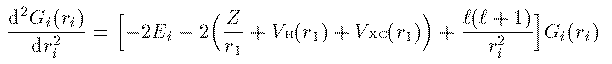 (19)
(19)
電子間Coulomb相互作用項
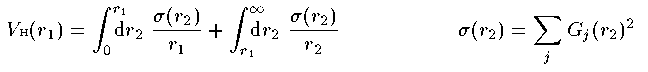 (20)
(20)
電子間交換相互作用項
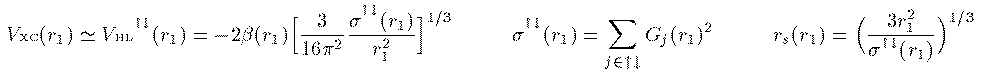 (21)
(21)
全エネルギー
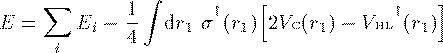
![]() (23)
(23)
動径波動関数は電子ごとにすべて異なるべきなのだが、計算を簡単化 するために動径波動関数はスピンと磁気量子数によらず、ただ主量子数と 方位量子数のみでラベルされると近似しよう。これで動径波動関数の数は 大幅に減少する。例えば Ne の10個の電子は3本の動径波動関数により 表される。ただし軌道の縮重度 g_i に気を付ける。 さらに、 Vhl^{↑↓} で、上下のスピンの電子密度を共に全電子密度の 半分として、 Vhl^{↑↓} を Vhl ひとつに近似しよう。すなわち、
である。これらの近似を制限付の方法と呼ぶ。Vc と Vhl は全電子の軌道波動関数の汎関数なので、 方程式は非常に複雑な連立方程式となっている。 この様な問題を解決する常套手段がSCF(Self Consistent Field)ループと 呼ばれる繰り返し計算である。
まず、 Vc と Vhl を 0 として φ_i と E_i を求める。これは 水素様原子の各準位を求める作業に他ならない。次に、得られた φ_i を 元に Vc と Vhl を計算する。この時の Vc と Vhl の変更分を 摂動として E_i を大雑把に更新する。そして φ_i と E_i を その時のpotentialの元でなるべく正確に解き直す。 この作業を繰り返していくと、 E_i の更新分は小さくなり、やがて 十分に自己矛盾のない(self consistentな) 解が得られる。
プログラムで用いる計算式を紹介する。 水素原子と同様に r=e^x と座標変換する。
電子間Coulomb相互作用項
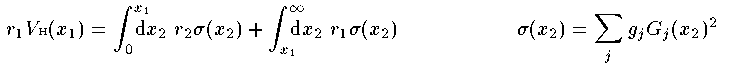 (27)
(27)
電子間交換相互作用項
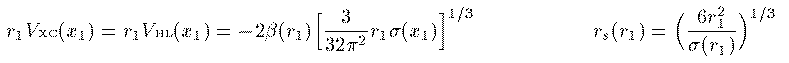 (28)
(28)
全エネルギー
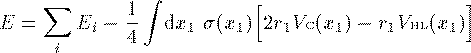 (29)
(29)
プログラムを作る準備が整った。ソースファイルは atom.ccである。 1電子方程式を解く関数群は水素原子の所で作成したものを利用するので、 多電子版として新たに付け加える部分のみを載せることにしよう。
まずは基本定数、外部変数の定義である。
const int ELE_NUM = 6; // number of electrons
const int ORB_NUM = 3; // number of orbitals
const double Z = (double)ELE_NUM; // atomic number
// 1S 2S 2P 3S 3P
const double g[] = { 2, 2, 2, 0, 0 }; // degeneracy of each orbitals
const int n[] = { 1, 2, 2, 3, 3 }; // quantum number of each orbitals
const int l[] = { 0, 0, 1, 0, 1 };
Orbital classのpropertyに軌道の縮重度を表す double g を 追加しよう。縮重度が整数でなく実数なのはイオン化エネルギーを計算する ためである。 今回はPotentialはSCFループで調整するものなので、その変化分に合わせて 軌道エネルギーを修正する次のmethodを Orbital classに追加しよう。
//---- modifies energy by first order perturbation Hamiltonian
void Orbital::Perturb( double dU[] )
{
for( int i=0 ; i<=R_FAR ; i++ ) E += sqr(G[i])*dU[i]*DX;
}
//---- represents density at given grid
double Orbital::Density( int i ){
return( g*sqr(G[i]) );
}
//---- represents energy of this orbital
double Orbital::Energy( void ){
return( g*E );
}
//---- represents energy of one electron in this orbital
double Orbital::OneEnergy( void ){
return( E );
}
Potentialを管理するclass Potential の設計が本プログラムでの 主題とも言えよう。いくつかのmethodが加わる。
Form() methodは密度汎関数法の1電子potentialをその時点での電子 波動関数から構築して U[] に設定するのだが、単純にそのものの値を U[] に代入するのではなく、前回に計算した U[] からの変化が 緩くなるな値を U[] に代入する。これは potentialの急進的な変更は SCFループの収束を不安定にしてしまうからである。 さらに、potentialの変化分を各軌道のobjectに通知して、 各軌道エネルギーを摂動で調整してもらう。
//---- modifies potential
void Potential::Form( void )
{
static double dU[R_NUM];
for( int i=0 ; i<=R_FAR ; i++ ){
dU[i] = 0.60*( -Z + UCoulomb(i) + UExchange(i) - U[i] );
U[i] += dU[i];
}
extern Orbital O[ORB_NUM];
for( int e=0 ; e<ORB_NUM ; e++ ) O[e].Perturb( dU );
}
//---- calculates coulomb term at given index
double Potential::UCoulomb( int i )
{
extern Orbital O[ORB_NUM];
int j, e;
double Uh, sigma;
for( j=0, Uh=0.0 ; j<=R_FAR ; j++ ){
for( e=0, sigma=0.0 ; e<ORB_NUM ; e++ ) sigma += O[e].Density(j);
if( j<i ) Uh += sigma * R[j]*DX;
else Uh += sigma * R[i]*DX;
}
return( Uh );
}
//---- calculates exchange term at given index
double Potential::UExchange( int i )
{
extern Orbital O[ORB_NUM];
int e;
double Uxc, sigma;
for( e=0, sigma=0.0 ; e<ORB_NUM ; e++ ) sigma += O[e].Density(i);
const double rs = cbrt(6.0*R[i]*R[i]/sigma);
const double be = 1.0 + 0.0368*rs*log(1.0+21.0/rs);
Uxc = -2*be*cbrt(3.0/(32*M_PI*M_PI)*R[i]*sigma);
return( Uxc );
}
//---- calculates total energy
double Potential::TotalEnergy( void )
{
extern Orbital O[ORB_NUM];
int e, i;
double Etot, sigma;
for( e=0, Etot=0.0 ; e<ORB_NUM ; e++ ) Etot += O[e].Energy();
for( i=0 ; i<=R_FAR ; i++ ){
for( e=0, sigma=0.0 ; e<ORB_NUM ; e++ ) sigma += O[e].Density(i);
Etot -= 0.25*sigma*(2*UCoulomb(i)+UExchange(i)) * DX;
}
return( Etot );
}
最後に main() 関数である。 各軌道を水素原子として初期化して、 SCFループでpotentailを構成して、各軌道を調整して、全エネルギーを 求める。その変化が十分に小さくなるまでSCFループを繰り返す。
//---- definition of fundermental
static Potential U;
static Orbital O[ORB_NUM];
//---- main function
int main( void )
{
double Etot, Epre;
int e;
for( e=0 ; e<ORB_NUM ; e++ ){
O[e].Assign( g[e], n[e], l[e] );
O[e].Adjust();
}
Etot = U.TotalEnergy();
do{ // SCF loop
U.Form();
for( e=0 ; e<ORB_NUM ; e++ ) O[e].Adjust();
Epre = Etot;
Etot = U.TotalEnergy();
}while( fabs(Etot-Epre)>1e-6 );
fprintf( stderr, "Total energy is %lf [a.u]\n\n", Etot );
for( e=0 ; e<ORB_NUM ; e++ ) O[e].Output();
return(0);
}
このプログラムが算出する種々の原子の電子のイオン化エネルギーと 全エネルギーを載せる。ただしイオン化エネルギーを求めるには軌道の 占有数を 0.5 だけ減らして再計算する若干の改造が必要である。
| Atom | 1S | 2S | 2P | Total Energy | |
| 1 | Hydrogen | 0.462716 | 0.448232 | ||
| 2 | Helium | 0.976619 | 2.836781 | ||
| 3 | Lithium | 2.478572 | 0.201917 | 7.336259 | |
| 4 | Beryllium | 4.659192 | 0.356338 | 14.447763 | |
| 5 | Boron | 7.527975 | 0.531178 | 0.310557 | 24.343309 |
| 6 | Carbon | 11.076859 | 0.722138 | 0.408769 | 37.422120 |
| 7 | Nitrogen | 15.308355 | 0.931399 | 0.509963 | 54.017180 |
| 8 | Oxygen | 20.223960 | 1.159927 | 0.615050 | 74.459528 |
| 9 | Fluorine | 25.824651 | 1.408207 | 0.724483 | 99.078869 |
| 10 | Neon | 32.111114 | 1.676504 | 0.838506 | 128.203954 |
より多電子の系を計算する場合には、より慎重に解かなくてはならない。 Form() method でのpotentialの更新をより緩やかに 更新するとうまくいく。セルの数や空間の範囲にも改良が必要である。 単純に広げるだけでは指数関数の効果により波動関数の値が 0 もしくは ∞ となり計算ができなくなるので注意が必要である。
多電子系の電子の準位で興味深い現象は 20番目の原子 Caの最外殻電子2つは3D軌道を空にして 4S軌道に入ることである。 この原因は、このような占有数の状態と、3D軌道を先に 詰めた占有数の状態の全エネルギーを計算して比較すれば明らかになる。 つまり、電子間の相互作用により、4S軌道に先に入る方が 全エネルギーがわずかに下がるのである。