● 電磁シャワー

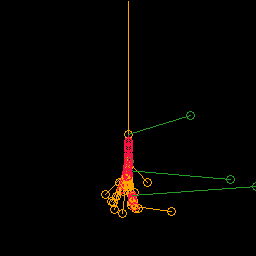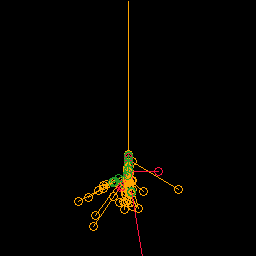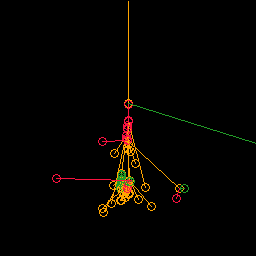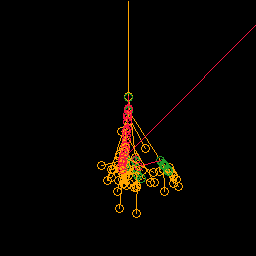
非常に高エネルギーの光子が宇宙から地球の大気に突入してくることが ある。この光子は大気中でさまざまな連鎖反応を起こし、大量の粒子を生成 する。粒子の飛散の様子から、この連鎖反応は電磁シャワー (Electromagnetic shower)と呼ばれている。 本節ではこの電磁シャワーを計算機の中で再現してみよう。 反応のプロセスは確率によって決まるので、まさにMonte Carlo法の 威力が発揮される問題である。

■ 反応の物理量の分布関数とサンプルの抽出法

反応のシミュレーションで必要な物理量は次の3種である。 反応までの自由行程、生成粒子のエネルギー、生成粒子の飛散方向。 これらの量はその分布関数からサンプルとして抽出される。 その分布関数は量子電磁力学(Quantum Electro Dynamics(QED))に よって導かれる。ここではこの理論が導いた分布関数をいかに利用するか を学ぶことにして、理論の詳細には立ち入らないことにする。

▲ 電磁シャワーの反応

制動放射(Bremsstrahlung)

高エネルギーの荷電粒子が物質中を走ると、 物質中の仮想光子と反応して減速して1個の光子を生成する。 100[MeV]以上の電子、陽電子ではこの反応が主反応である。

対生成(pair production)

1[MeV]以上の光子が物質中を走ると、 物質中の仮想光子と反応して消滅して電子と陽電子を生成する。

対消滅(pair annihilation)

陽電子が物質中を走ると、物質中の電子と反応して消滅して2個の光子を 生成する。高エネルギーの陽電子は滅多に電子と衝突しないのでこの反応は 珍しい。陽電子の速度が十分遅くなると、周りの電子に引き寄せ られ対消滅反応が起こりやすくなる。

この3つの反応で実際の電磁シャワーを表すことができるのは 粒子のエネルギーが 100[MeV]以上の場合に限られる。 反応によってより低いエネルギーの粒子が生じた場合、その粒子の 反応については一切扱わないことにする。

▲ 全反応断面積

全反応断面積(total cross section) σは入射する粒子が衝突して 反応する物質のいわば 的の面積である。この値と標的の密度により反応の起こる確率が求まり、 粒子の自由行程も求まる。 この3種の反応の全反応断面積はQEDにより導かれているが、さらに簡単な 以下の近似式を用いる。

制動放射 (1)

対生成 (2)

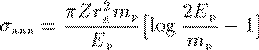対消滅 (3)

(1)式の E_{g,min} は制動放射で放射される光子の 最低エネルギーであり 100[keV] 程度であることが知られている。

▲ 自由行程のサンプル抽出

物質がつまった単位断面積の筒の中を粒子が通過することを考える。 筒の薄い区間に全反応断面積 σ の的が dN 個あれば、 この区間を粒子が的に当たらずに通過する確率は 1-σdN である。

dN を一定値として筒を薄い区間に分割すると、粒子が N個の的を 避けて通過できる確率は (1-σ dN)^{N/dN} である。 dN を十分小さく、Nを十分大きくとれば、これは指数関数 exp(-σN) となる。よって粒子が N 個の所まで通過して、 N+dN 個の所で的に当たって反応を起こす確率 f(N)dN は

(4)

(5)
(6)

(7)

(8)

制動放射 (9)

対生成 (10)

対消滅 (11)

1. 第一因子の確率分布に従う ε のサンプルを逆変換法の次式により 一様乱数から得る。

   (12)

2. その ε による第二因子の値が新たな一様乱数の値より 大きいならばその ε を採用し、小さいならば棄却して 1の行程 に戻る。これが棄却法である。

(13)

1. 項の重みに応じて1つの項を選択する。つまり、 9:d で変数 b を b=a または b=3a に選ぶ。
2. 選択した項を分布関数として2次元の逆変換法を使う。 2つの一様乱数 r_1, r_2 から次式で u のサンプルを得る。

   (14)

3. uから polar angleを求めて、それが [0,π] の範囲内にあればサンプルを採用し、なければ 1の行程に戻る。

(15)
(16)
(17)

(18)
(19)
(20)

(21)
(22)
(23)
(24)

ソースファイルはshower.cc である。 プログラムの始めはいつも通り諸定数の定義と簡単なinline関数の 定義である。

#include "cip.h"
#include "nxgraph.h"

//---- definition of fundermental constants
//---- air setting
const double Z_AIR       = 7.2;           // mean atomic number of atom in air
const double LN_Z_AIR    = 2.00;          // log(Z_AIR)
const double A_AIR       = 14.4;          // mean mass number of atom in air
const double RHO_AIR     = 1.2;           // density of air [g/little]==[kg/m^3]
const double C_AIR       = 1.4e-4;        // factor of rho decresing [1/m]
const double SIGMA_O     = ALPHA*Z_AIR*Z_AIR*R_E*R_E;  // don't edit
const double FACT_Z      = 5.21-LN_Z_AIR/3.0;          // don't edit

//---- experimental setting
const double INIT_PHOTON_HEIGHT  = 5e4;   // [m]
const double INIT_PHOTON_ENERGY  = 1e3;   // [MeV]
const double ENERGY_CUTOFF       = 1e2;   // least energy [MeV], below thie energy, particles are treated as dead
const double BREMS_CUTOFF = 0.1;          // least photon energy radiated by br
const double FAR_AWAY            = 1e5;   // long distance [m]

//---- particle type indicators
const int    PHOTON       = 0;
const int    ELECTRON     = 1;
const int    POSITRON     = 2;
//---- reaction indicators
const int    FATE_NON     = 0;
const int    FATE_BRE     = 1;
const int    FATE_PRO     = 2;
const int    FATE_ANN     = 3;
//---- graphics settings
const int    WIN_HEIGHT   = 256;
const int    WIN_WIDTH    = 256;
const int    GROUND_HEIGHT= 16;
const double YMAG         = (WIN_HEIGHT-GROUND_HEIGHT)/INIT_PHOTON_HEIGHT;
const double XMAG         = YMAG*256;

//---- Density of the air at given height
inline double N_AIR( double h ){
  return( (RHO_AIR*1000/A_AIR*N_A)*exp(-h*C_AIR) );
}
//---- transform real coordinates into window coordinates
inline int Wx( double x, double y, double z ){
  return( WIN_WIDTH/2 + int(XMAG*(CV*x-SV*y)) );
}
inline int Wy( double x, double y, double z ){
  return( WIN_HEIGHT - GROUND_HEIGHT - int(YMAG*z) + int((XMAG/8)*(SV*x+CV*y)) );
}

Position クラスは粒子の位置を3次元デカルト座標で記録し、 その足し上げ演算 operator += を定義する。

//---- definition of class Position
class Position
{
public:
  double x, y, z;
  inline Position( void ){}
  inline Position( const double& _x, const double& _y, const double& _z ){
    x = _x;    y = _y;    z = _z;
  }
  inline void operator+=( const Position& _r ){
    x += _r.x;    y += _r.y;    z += _r.z;
  }
};

//---- definition of class Direction
class Direction
{
public:
  double norm;
  double rot[3][3];
  Direction( void ){};
  Direction( double _norm, double _theta, double _phi ){
    norm  = _norm;
    double ct = cos(_theta),    st = sin(_theta);
    double cp = cos(_phi),      sp = sin(_phi);
    rot[0][0] = +ct*cp;    rot[0][1] = -sp;    rot[0][2] = st*cp;
    rot[1][0] = +ct*sp;    rot[1][1] = +cp;    rot[1][2] = st*sp;
    rot[2][0] = -st   ;    rot[2][1] =   0;    rot[2][2] = ct   ;
  }
  inline Position operator*( const double& k ){
    return( Position( rot[0][2]*k, rot[1][2]*k, rot[2][2]*k ) );
  }
  Direction& Turn( const Direction& _dir ){
    double t[3][3];
    int i, j, k;
      // multiply matrix rot[][] by given _dir's matrix
    for( i=0 ; i<3 ; i++ ){
      for( j=0 ; j<3 ; j++ ){
        t[i][j] = 0.0;
        for( k=0 ; k<3 ; k++ ){
          t[i][j] += _dir.rot[i][k] * rot[k][j];
        }
      }
    }
       // update matrix rot[][]
    for( i=0 ; i<3 ; i++ ){
      for( j=0 ; j<3 ; j++ ){
        rot[i][j] = t[i][j];
      }
    }
    return( *this );
  }
};

operator * は与えられた空間の長さのその方向の3次元ベクトルを 返す。

method Turn() は自身のobjectの回転行列に、引数に与えられた 別なobjectの回転行列を掛け合わせることで、2つの方向を足し合わせる。 つまり、右上の図の様に (θ',φ') として 生成粒子の方向を親粒子を基準として設定し、 親粒子の絶対的な方向 (θ,φ) を記録するobjectを 生成粒子の Turn() methodに 与えると生成粒子の絶対的な方向が計算されるわけである。

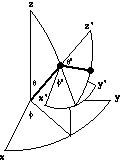
親粒子の絶対方向と生成粒子の親粒子の方向に対する相対方向

光子、電子、陽電子の3種の粒子のさまざまな管理を行うclassを設計する ことになるのだが、それらの管理方法は多くの部分で共通した仕組みとなり そうである。そこで共通する仕組みを提供する基本クラスをまず設計する。 名付けて Particle classである。まずその宣言部を見てみよう。

//---- declaration of class Particle
class Particle
{
protected:
  char      type;                    // particle name
  char      fate;                    // reaction
  u_long    color;                   // color

  Position  ri, rf;                  // initial and final position
  Direction dir;                     // direction and energy
  double    free_path;               // length of its free path
  Particle* next;                    // pointer to next particle
public:
       Particle( const Position& _r, const Direction& _dir, Particle* _next=NULL );
  virtual ~Particle( void );
  void Evolve( void );
protected:
  double  FreePath( double sigma );
  virtual void Reaction( void )=0;
  void Draw( void );
private:
  void CheckAlive( void );
};

• type はこの粒子の種類を記録するが、このプログラムでは 使われていない。
• fate はこの粒子が将来起こす反応の種類を記録する。 反応が起こらずに終ることもひとつの反応として扱う。
• color はこの粒子の飛跡を描く際の色を記録 する。
• ri, rf はこの粒子の生成位置と反応位置を記録する。
• dir はこの粒子の放射方向とエネルギーを記録する。 Position型とDirection型は別に宣言する特別なclassである。
• free_path はこの粒子の自由行程を記録する。
• next はリンクリストでのこの粒子の次の粒子のアドレスを記録する。

次に methodを紹介しよう。

Particle() constructorは与えられた引数でこの粒子の各propertyを 初期化するだけで特に計算はしない。

//---- base constructor
Particle::Particle( const Position& _r, const Direction& _dir, Particle* _next ){
  rf = ri = _r;    dir = _dir;    next = _next;
}

//---- recursive destructor
Particle::~Particle( void ){
  if( next ) delete next;
}

//---- calculate length of free path
double Particle::FreePath( double sigma )
{
  double a = -C_AIR*dir.rot[2][2];  // factor of decreasing density toward this direction.
  double n = -log(Urand0())/sigma;   // number of targets
  double r = 1+n*a/N_AIR(ri.z);     // temporal value
  if( r<0 ) return( FAR_AWAY );     // r<0 means the particle goes back to the universe
  return( log(r)/a );
}

Evolve() methodはこの粒子をその生成地点から消滅地点まで 時間発展させ、 CheckAlive() methodにその粒子の生存を確認させ、 Reaction() methodに反応を起こさせる。さらに再帰的に次の粒子の Evolve() methodを呼び出す。これにより全粒子の時間発展が行われる ことになる。 Draw() methodは粒子の軌跡を再帰的に絵がく。

//---- recursive evolve
void Particle::Evolve( void )
{
  rf += dir*free_path;
  CheckAlive();
  Reaction();
  if( next ) next->Evolve();
}

CheckAlive() methodはこの粒子のエネルギーが既定値を下回ったか、 地面に到達したかなどをチェックして、もしそうなら これ以上反応を起こさせないようにproperty fate を設定する。

//---- check whether this particle is still alive
void Particle::CheckAlive( void ){
  if( rf.z < 0 || dir.norm < ENERGY_CUTOFF ) fate = FATE_NON;
} 

//---- draw trace of particle from birth point to reaction point
void Particle::Draw( void )
{
  int xi = Wx( ri.x, ri.y, ri.z ),  yi = Wy( ri.x, ri.y, ri.z );
  int xf = Wx( rf.x, rf.y, rf.z ),  yf = Wy( rf.x, rf.y, rf.z );
  NXSetColor( color );
  NXDrawLine(   xi, yi, xf, yf );
  NXDrawCircle( xf, yf, 4 );

  if( next ) next->Draw();
}

//---- declaration of class Photon
class Photon : public Particle
{
public:
  Photon( const Position& _r, const Direction& _dir, Particle* _next=NULL );
private:
  void Reaction( void );
  void PairProduction( void );
};

//---- declaration of class Electron
class Electron : public Particle
{
public:
  Electron( const Position& _r, const Direction& _dir, Particle* _next=NULL );
private:
  void Reaction( void );
  void Bremsstrahlung( void );
};

//---- declaration of class Positron
class Positron : public Particle
{
public:
  Positron( const Position& _r, const Direction& _dir, Particle* _next=NULL );
private:
  void Reaction( void );
  void PairAnnihilation( void );
  void Bremsstrahlung( void );
};

Reaction() methodは基本classで純粋仮想methodとして宣言して おいたので派生classで具体的な内容が与えられることが期待されている。 Reaction() methodは fate に従って反応の計算を行う methodを呼び出す。反応が起きない状況では何も呼び出さずに終る。

Bremsstrahlung() 、 PairAnnihilation() 、 PairProduction() のmethod はその名の通り反応の具体的な計算を 行い、生成粒子の変数を動的確保しリンクリストに追加する。この 操作がこのプログラムの要となっている。対生成の場合のこの操作を示す。

next = new Electron( rf, dir_e, next );
next = new Positron( rf, dir_p, next );

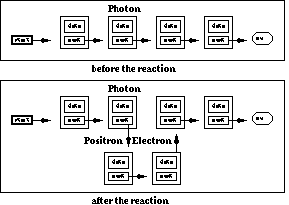
生成粒子のリンクリストへの登録

反応がすべて終了したらデータ収集を行うのだがこの例では 省略している。最後に delete を走らせてメモリを解放する。 派生粒子classのmethodの内容を以下に示す。

//---- definition of methods under class Photon
//---- constructor for photon
Photon::Photon( const Position& _r, const Direction& _dir, Particle* _next ):Particle( _r, _dir, _next )
{
  type      = PHOTON;
  color     = NX_ORANGE;

  free_path = FreePath( (28.0/9.0)*SIGMA_O*FACT_Z );
  fate      = FATE_PRO;
}

//---- select reaction
void Photon::Reaction( void )
{
  switch( fate ){
    case FATE_PRO : PairProduction(); break;
  }
}

//---- let photon react pair production
void Photon::PairProduction( void )
{
  double eps;                    // friction of energy carried by radiated electron
  double Ene_g  = dir.norm;      // energy of parent photon
  double Ene_1, Ene_2;           // energys of electron and positron
  double the_1, the_2;           // polar angles of each particles
  double phi_1, phi_2;           // azimuthal angles of each particles

    // get a sample of radiation energy
  double epso   = M_ELE/Ene_g, lnepso = log(epso);
  do{ eps = epso*exp(-Urand()*lnepso); }while( !(Urand() < eps-1+3.0/(4.0*eps) ) );
  Ene_1 = Ene_g*eps;

    // get a sample of radiation angle
  double A = 1.6*M_ELE/Ene_1, double D = 3.0;
  do{
    if( Urand()<1.0/(1.0+D) ) the_1 = -log(Urand0()*Urand0())*A;
    else                      the_1 = -log(Urand0()*Urand0())*A/3;
  }while( !(the_1 < M_PI) );
  phi_1 = 2*M_PI*Urand();

    // calculate about another particle
  Ene_2 = hypot( Ene_1*sin(the_1), Ene_g-Ene_1*cos(the_1) );
  the_2 = atan2( Ene_1*sin(the_1), Ene_g-Ene_1*cos(the_1) );
  phi_2 = phi_1 - M_PI;

    // prepare new direction
  Direction dir_1( Ene_1, the_1, phi_1 );
  Directionn dir_2( Ene_2, the_2, phi_2 );
    // make child particles
  if( Urand() < 0.5 ){  // determine whether No.1 particle is electron or positron
    next = new Electron( rf, dir_1.Turn( dir ), next );
    next = new Positron( rf, dir_2.Turn( dir ), next );
  }else{
    next = new Positron( rf, dir_1.Turn( dir ), next );
    next = new Electron( rf, dir_2.Turn( dir ), next );
  }
}
  
//---- definition of methods under class Electron
//---- constructor for electron
Electron::Electron( const Position& _r, const Direction& _dir, Particle* _next ):Particle( _r, _dir, _next )
{
  type      = ELECTRON;
  color     = NX_GRASS;
  free_path = FreePath( (16.0/3.0)*SIGMA_O*FACT_Z*(log(dir.norm/BREMS_CUTOFF)-0.0625) );
  fate      = FATE_BRE;
}

//---- select reaction
void Electron::Reaction( void )
{
  switch( fate ){
    case FATE_BRE: Bremsstrahlung(); break;
  }
}

//---- let electron react bremsstrahlung
void Electron::Bremsstrahlung( void )
{
  double eps;                    // friction of energy carried by radiated photon
  double Ene_e  = dir.norm;      // energy of parent electron
  double Ene_g, Ene_d;           // energys of photon and decerated electron
  double the_g, the_d;           // polar angles of each particles
  double phi_g, phi_d;           // azimuthal angles of each particles

    // get a sample of radiation energy
  double epso   = BREMS_CUTOFF/Ene_e, lnepso = log(epso);
  do{ eps = epso*exp(-Urand()*lnepso); }while( !(Urand() < (4.0/3.0)*eps*eps - eps + 1.0 ) );
  Ene_g = Ene_e*eps;

    // get a sample of radiation angle
  double A = 1.6*M_ELE/Ene_e, D = (1.16+1.88/Z_AIR)*(1+eps);
  do{
    if( Urand()<1.0/(1.0+D) ) the_g = -log(Urand0()*Urand0())*A;
    else                      the_g = -log(Urand0()*Urand0())*A/3;
  }while( !(the_g < M_PI) );
  phi_g = 2*M_PI*Urand();

    // calculate about another particle
  Ene_d = hypot( Ene_g*sin(the_g), Ene_e-Ene_g*cos(the_g) );
  the_d = atan2( Ene_g*sin(the_g), Ene_e-Ene_g*cos(the_g) );
  phi_d = phi_g - M_PI;

    // prepare new direction
  Direction dir_d( Ene_d, the_d, phi_d );
  Direction dir_g( Ene_g, the_g, phi_g );
    // make child particles
  next = new Electron( rf, dir_d.Turn( dir ), next );
  next = new Photon(   rf, dir_g.Turn( dir ), next );
}


//---- definition of methods under class Positron
//---- constructor for positron
Positron::Positron( const Position& _r, const Direction& _dir, Particle* _next ):Particle( _r, _dir, _next )
{
  double gamma, path_ann, path_bre;

  type     = POSITRON;
  color    = NX_RED;
  gamma    = dir.norm/M_ELE;
  path_ann = FreePath( M_PI*Z_AIR*R_E*R_E*(log(2*gamma)-1)/gamma );
  path_bre = FreePath( (16.0/3.0)*SIGMA_O*FACT_Z*(log(dir.norm/BREMS_CUTOFF)-0.0625) );
  
  if( path_ann < path_bre ){
    free_path = path_ann;    fate      = FATE_ANN;
  }else{
    free_path = path_bre;    fate      = FATE_BRE;
  }
}

//---- select reaction
void Positron::Reaction( void )
{
  switch( fate ){
    case FATE_BRE: Bremsstrahlung();   break;
    case FATE_ANN: PairAnnihilation(); break;
  }
}

//---- let electron react bremsstrahlung
void Positron::Bremsstrahlung( void )
{
  double eps;                    // friction of energy carried by radiated photon
  double Ene_p  = dir.norm;      // energy of parent positron
  double Ene_g, Ene_d;           // energys of photon and decerated positron
  double the_g, the_d;           // polar angles of each particles
  double phi_g, phi_d;           // azimuthal angles of each particles

    // get a sample of radiation energy
  double epso   = BREMS_CUTOFF/Ene_p, lnepso = log(epso);
  do{ eps = epso*exp(-Urand()*lnepso); }while( !(Urand() < (4.0/3.0)*eps*eps - eps + 1.0 ) );
  Ene_g = Ene_p*eps;

    // get a sample of radiation angle
  double A = 1.6*M_ELE/Ene_p, D = (1.16+1.88/Z_AIR)*(1+eps);
  do{
    if( Urand()<1.0/(1.0+D) ) the_g = -log(Urand0()*Urand0())*A;
    else                      the_g = -log(Urand0()*Urand0())*A/3;
  }while( !(the_g < M_PI) );
  phi_g = 2*M_PI*Urand();

    // calculate about another particle
  Ene_d = hypot( Ene_g*sin(the_g), Ene_p-Ene_g*cos(the_g) );
  the_d = atan2( Ene_g*sin(the_g), Ene_p-Ene_g*cos(the_g) );
  phi_d = phi_g-M_PI;

    // prepare new direction
  Direction dir_d( Ene_d, the_d, phi_d );
  Direction dir_g( Ene_g, the_g, phi_g );
    // make child particles
  next = new Positron( rf, dir_d.Turn( dir ), next );
  next = new Photon(   rf, dir_g.Turn( dir ), next );
}

//---- let positron react pair annhilation
void Positron::PairAnnihilation( void )
{
  double eps;                    // friction of energy carried by one photon
  double Ene_p   = dir.norm;     // energy of parent positron
  double Ene_g1, Ene_g2;         // energys of radiated photons
  double the_g1, the_g2;         // polar angles of radiated photons
  double phi_g1, phi_g2;         // azimuthal angles of radiated photons

    // get a sample of radiation energy
  double epso   = M_ELE/(2*Ene_p), lnepso = log(epso);
  do{ eps = epso*exp(-Urand()*lnepso); }while( !(Urand() < 1-eps) );
  Ene_g1 = Ene_p*(eps);
  the_g1 = acos( 1.0 - (1.0-eps)/((eps)*Ene_p/M_ELE) );
  phi_g1 = 2*M_PI*Urand();

    // calculate about another particle
  Ene_g2 = Ene_p*(1-eps);
  the_g2 = acos( 1.0 - (eps)/((1.0-eps)*Ene_p/M_ELE) );
  phi_g2 = phi_g1-M_PI;

    // prepare new direction
  Direction dir_g1( Ene_g1, the_g1, phi_g1 );
  Direction dir_g2( Ene_g2, the_g2, phi_g2 );
    // make child particles
  next = new Photon( rf, dir_g1.Turn( dir ), next );
  next = new Photon( rf, dir_g2.Turn( dir ), next );
}

int main( void )
{
  XEvent ev;
  NXOpenWindow( "Elemag Shower", WIN_WIDTH, WIN_HEIGHT );
  NXEnable( NX_DOUBLEBUFFER );

  Position   r( 0, 0, INIT_PHOTON_HEIGHT );
  Direction  dir( INIT_PHOTON_ENERGY, M_PI, 0 );

  do{
    Particle* parent = new Photon( r, dir );
    parent->Evolve();

    NXClearWindow();
    parent->Draw();
    NXFlush();

    delete parent;
  }while( NXCheckEvent( NX_WAIT, ev ) != KeyPress );

  NXCloseWindow();
  return(0);
}