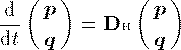 (1)
(1)Symplectic数値積分法は近年登場した超高精度の数値積分法で ある。その導出法が特殊なことからまだあまり普及していないが、その 使い方は至って簡単であり、近い将来多くの分野でこのSymplectic法が 使われるであろう。 このSymplectic数値積分法の原理と構築方法、実際の物理 シミュレーションでの利用の仕方を学ぼう。
議論を簡単にするため 1質点系の運動を考えるが、 この議論は多体系にもそのまま拡張することができる。
物体の運動量 p(t) と位置 q(t) の時間変化は、大抵の問題において 次のような形の微分方程式によって支配される。
ここで Dh は抽象的な演算子であり、与えれた (p,q) を その時間変化分に変換する演算子とする。演算子 Dh は p,q に対して形式が不変な演算子であり、 この微分方程式においては定数として扱うことができる。 そのため、この微分方程式の解は抽象的に次のように表される。
つまり、この Dh は系の時間推進演算子の生成子であることがわかる。 (2)式は抽象的な系の厳密解である。初期値 p(0),q(0) から任意の時刻 t での値 p(t),q(t) がこの式より求まるが、実用では この時間 t を短い時間 Δt に置き換えて、 p(Δt),q(Δt) を求めて、それを再び初期値として 次のステップでの値を求める方法をとる。 しかし (2)式は抽象的なため、 具体的な計算にはとりかかれない。
p,q の時間変化をもたらす物理的要素には、例えば運動エネルギーによる 要素、ポテンシャル力、摩擦力、相互作用力などの複数の要素があり、個々の 要素がもたらす時間変化分の和が、系の時間変化分となる。
演算子 Dh は (p,q) の時間変化分を導く演算子であるが、 この演算子もまた、個々の物理的要素による時間変化分を導く演算子の 和と考えることができる。議論をさらに簡単にするために、運動エネルギー の効果による演算子 Dk とポテンシャル力の効果による演算子 Du みの系を考える。つまり、もっとも単純な粒子の運動であり、
である。(3)式の右辺の演算子の和の指数を演算子の 指数の積に近似展開することを考えよう。 t の1次の近似では次のように展開される。 t の2次の近似では次のように展開される。 このように各演算子を単独で時間推進演算子の生成子に仕立て上げる ことが重要な意味をもつことはすぐ後でわかる。分解された各生成子による時間推進演算子の意味は次の通りである。
exp[Δt Dk] は運動エネルギーの効果のみの系の時間推進を表す。 すなわち自由空間での運動である。よって p は不変であり位置 q が 等速直線運動として変化する。これは厳密に計算することが可能である。
exp[Δt Du] はポテンシャル力 Fu がもたらす p の時間発展の 効果を表す。q は変わらない。保存力は p に依らないので Fu は定数となる。これもまた厳密に計算することが可能である。 Symplectic法は、(4)式、(5)式 などの指数積展開の式に 従ってこの2種の時間発展作業を順番に行う数値積分法なのである。 指数積展開に n 次近似式を用いた方法を n 次Symplectic数値積分法と呼ぶ。なぜこれだけの手順で超高精度の結果が得られるのであろうか。
exp{[Δt Dk]}、exp{[Δt Du]}の各時間推進演算子は 単独で厳密な時間発展を計算するが 1次Symplectic法でのその2つの積 exp{[Δt Dk]} exp{[Δt Du]} は何を意味しているのだろうか。
BHCの公式から次の関係を満たす生成子 Dh' が存在することがわかる。
この左辺の各因子の時間発展を厳密に行うことは、 右辺の生成子 Dh' が支配するような系の時間発展を 厳密に行うことなのである。 生成子 Dh' は元の生成子 Dh とは展開の際の近似の分だけ 異なっている。つまり、この2つの系のHamiltonianの違い、すなわち エネルギーの違いは指数積展開の際の近似の程度、O(Δt^{n+1})である。Dh' の系でのエネルギーは時間発展が厳密なので保存される。 従って Dh の系のエネルギーは保存されるべき真の値から わずか O(Δt^{n+1}) 程度ずれるだけで、その精度を永久に保つのである。 要約すればSymplectic法は、系をわずかに変換して、 厳密可積分系とし、これを厳密に積分する方法なのである。 これがSymplectic法の他に類を見ない特徴である。
Symplectic法は位置や運動量などの保存量ではない物理量の厳密さまでは 保証しないが、エネルギーが超高精度に保存されるので他の物理量の信頼性も著しく高い。
論より証拠、Symplectic法の威力を確かめるために 簡単なシミュレーションプログラムを作ってみよう。
N個の質点が重力を及ぼしあって運動する系をシミュレーション してみよう。 N=3の系はいわゆる3体問題と呼ばれ、代数的には解けないことで有名 である。より多くの多体系はなおさらである。
例として、4個の星が円周上に等間隔で並んで円周上をまわる連成系を 扱おう。簡単のため運動は2次元平面内に限定する。 次の形式の2次のSymplectic法を用いる。
最後の因子は形式をそろえるためだけである。 各時間推進の演算子の効果は次の通りとなる。 形式的には、p,q,f は2N次元のベクトルであるが、 計算の際には個々の星について2次元ベクトルで計算する。プログラムは比較的簡単である。 ソースファイルは star.cc である。 まず諸定数を設定する。
単位系はかなり適当である。 星の運動量や位置などの情報を束ねて構造体として管理しよう。#include "cip.h" #include "vector2.h" //---- physical constants const double Mstar = 1.0; // mass of a star const double G = 1.00; // Gravity constant //---- experimental settings const double dT = 1.0/256; // temporal step const int N = 4; // number of stars
//---- declaration of structure Matter
struct Matter
{
Vector2 p, q, f; // momentum, position, force
};
const int symp_r = 2;
const double symp_k[2] = {
+0.500000000000000,
+0.500000000000000
};
const double symp_u[2] = {
+0.000000000000000,
+1.000000000000000
};
Init() 関数は星の初期値を設定する。
//---- initialize properties of stars
void Init( Matter M[] )
{
for( int n=0 ; n<N ; n++ ){
// locate stars on circumference
double ang = 2*M_PI/N*n;
M[n].p = Vector2( -sin(ang), cos(ang) );
M[n].q = Vector2( cos(ang), sin(ang) );
}
}
//---- calculates gravity force amoung two stars
Vector2 Interaction( Matter& M1, Matter& M2 )
{
const Vector2 vec_r = M1.q - M2.q;
const double r = abs(vec_r);
return( -G*Mstar*Mstar/(r*r*r) * vec_r );
}
//---- calculates gravity field
void CalcField( Matter M[] )
{
int n1, n2;
// reset M[].f
for( n1=0 ; n1<N ; n1++ ){
M[n1].f = Vector2( 0.0, 0.0 );
}
// sums up M[].f
for( n1=0 ; n1<N ; n1++ ){
for( n2=n1+1 ; n2<N ; n2++ ){
Vector2 f = Interaction( M[n1], M[n2] );
M[n1].f += f;
M[n2].f -= f; // Newton's law "The third law of motion"
}
}
}
//---- calculates total energy
double CalcEnergy( Matter M[] )
{
int n1, n2;
double E;
// sums up energy
for( n1=0, E=0.0 ; n1<N ; n1++ ){
E += (1.0/(2*Mstar))*abs2(M[n1].p); // Kinetic Energy
for( n2=n1+1 ; n2<N ; n2++ ){
E += -G*Mstar*Mstar/abs(M[n1].q-M[n2].q); // Potential Energy
}
}
return( E );
}
//---- main function
int main( void )
{
int n;
Matter M[N];
Init( M );
for( double T=0.0 ; T<10.0 ; T += dT ){
// symplectic steps
for( int r=0 ; r<symp_r ; r++ ){
CalcField( M );
for( n=0 ; n<N ; n++ ){ // Potential term
M[n].p += dT*symp_u[r] * M[n].f;
}
for( n=0 ; n<N ; n++ ){ // Kinetic term
M[n].q += dT*symp_k[r] * (1.0/Mstar) * M[n].p;
}
}
printf("%lf %lf\n", T, CalcEnergy(M) );
}
return(0);
}
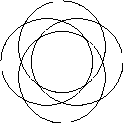
このプログラムが計算する4連星の軌道
重力は引力であるため、星が異常に接近することがある。その場合、 加速度が大きくなりすぎてSymplectic法でも正確に計算できなくなる。 これに対処するには加速度に応じて時間刻 dT を自動調整する ように設計したり、衝突による跳ね返りを起こしたりしなくてはならない。
星の多体運動の次は電子の多体運動をシミュレーションしてみよう。 電子同士はクーロン斥力で反発するが、さらに外から静磁場 B を z軸の向きにかける。i番目の電子の運動方程式は次の通りである。
ここに E_i はi番目の電子に作用する他の電子のクーロン 斥力による電場である。 時間推進演算子の生成子 Dhには磁場による項 Db が加わることになる。 3つの項の和の指数積もそれぞれの指数の積に分解する事は容易にできるが、 ここでは、そうはせずに、Dk+Db をまとめて一つの演算子として 扱う。なぜなら、この演算子の意味するところは電場が無く一様磁場のみの 系での電子の運動である。この系の時間幅 Δt での時間発展は 代数的に容易に答えが得られて、 ここでωはLarmor周波数 ω=eB/m である。 結局、この系でもSymplectic法は系を厳密可積分系に変換できる。プログラムの要となる部分のみを載せておく。 ソースファイルは electrons.cc である。
//---- physical constants
const double Mele = 1.0; // mass of an electron
const double Eele = 1.0; // charge of an electron
const double Aint = 1.0; // coupling constant of ele-ele interaction
const double Bext = 2.0; // external magnetic field
const double Omega = Eele*Bext/Mele; // Larmor anglur frequency
//---- calculates electric force amoung two electrons
inline Vector2 Interaction( Matter& M1, Matter& M2 )
{
const Vector2 vec_r = M1.q - M2.q;
const double r = abs(vec_r);
return( Aint*Eele*Eele/(r*r*r) * vec_r );
}
//---- calculates total energy
double CalcEnergy( Matter M[] )
{
int n1, n2;
double E;
// sums up energy
for( n1=0, E=0.0 ; n1<N ; n1++ ){
E += 0.5/Mele*abs2(M[n1].p); // kinetic energy
for( n2=n1+1 ; n2<N ; n2++ ){
E += Aint*Eele*Eele/abs(M[n1].q-M[n2].q); // potential energy
}
}
return( E );
}
//---- main function
int main( void )
{
int n;
Matter M[N];
Init( M );
for( double T=0.0 ; T<500.0 ; T += dT ){
for( int r=0 ; r<symp_r ; r++ ){
CalcField( M );
for( int n=0 ; n<N ; n++ ){ // potential term
M[n].p += dT*symp_u[r] * M[n].f;
}
for( n=0 ; n<N ; n++ ){ // kinetic and Magnetic term
double co = cos(Omega*dT*symp_k[r]);
double si = sin(Omega*dT*symp_k[r]);
M[n].q.x += (1.0/(Mele*Omega))*( M[n].p.x*si - M[n].p.y*(1-co) );
M[n].q.y += (1.0/(Mele*Omega))*( M[n].p.x*(1-co) + M[n].p.y*si );
double p_x = M[n].p.x;
M[n].p.x = p_x*co - M[n].p.y*si;
M[n].p.y = p_x*si + M[n].p.y*co;
}
}
printf("%lf %lf\n", T, CalcEnergy(M) );
}
return(0);
}

このプログラムが計算する磁場中の4電子の軌道
このプログラムもまた電子の軌跡をWindowに描くと楽しい。
外から一様な電場をxy平面内に加えて、電子間相互作用より十分強くすると 電子は回転しながら電場と磁場と垂直な方向へ移動する。 電子を加速しているので当然エネルギーは増加する が電場の仕事の分も加味した全エネルギーは保存される。 電子に摩擦力を働かせるようにすると電場の向きと逆(本来電子が進む方向) に少し動くようになる。摩擦力のため系のエネルギーは減少するが 散逸した分も加味した全エネルギーは保存される。
指数積をΔt のより高次の項まで考慮して展開する高次Symplectic法の 構築方法は近年までは難しい技術であった。 それが1990年代に入って東京大学物理教室の鈴木増雄先生により任意に高次の 指数積展開法が開発され、いくらでも超高精度の高次Symplectic法が手軽に 構築できるようになったのである。その構築法のひとつをここで簡単に 紹介する。
なんらかの作用素 A,Bの和の指数 exp[A+B] を exp[A]とexp[B]の積で近似することが目的である
A+Bは自分自身とは可換であるため 任意の数 s_3 に対して次の恒等式が成り立つ。
この積の中の第1因子を (A+B) について作用素の3次の項まで Taylor展開する。 第2、第3因子についても同様に展開して、それらを (16)式に 代入することを考える。整理した結果、その表式のうち作用素の3次の項 は次の通りである。 ここで s_3に次の関係を満たさせる。 すると、(16)式には作用素の3次の項が 無くなることになる。ところで、作用素の2次の項まで正確に近似した次式
これはこれまでの例で使われてきた分解表式である。 この表式をO(3)を含めたまま(16)式の各因子に用いると となるが、ここでs_3が(19)式の関係を満たすならば、 [作用素の3次の項]は0である。従って (22)(23)式は事実上 作用素の3次の項まで正確に近似した次式に他ならない。すなわち、 である。3次近似展開が完成したら同様な論理でより高次の近似展開が 次々に構築される。これが鈴木先生が提唱された高次展開の構築の基本戦略 である。m次近似 S_{m} はm-1近似 S_{m-1} により次の様に構築される。 ところが詳しく調べるとこの分解の場合、奇数次の近似展開 S_{2m-1} は作用素の 2m 次まで正しく近似していることがわかる。つまり、 このひとつ高次の偶数次の近似展開 S_{2m}と同じなのである。 従って、次のように偶数次の近似展開だけでを用いて少ない因子数で 高次の近似展開を構築できる。 こうして高次の近似展開を最初の S_2 の掛け合わせで構築できる。 すなわち、指数積展開が任意の次数まで可能になり、さらに 任意の次数のSymplectic法が構築されるのである。(30)-(32)式による4次と6次のSymplectic法の ための係数をファイル symplectic.h に 載せておく。
係数の中には負の値を持つものや1以上の値を持つものがある。 負の展開係数は時間をさかのぼる積分になる。1を越える展開係数は Δt の1ステップより大きな幅で積分することになり精度上あまり よろしくない。 展開係数が小さな値となる次のタイプの指数積の展開法がある。
この(33)-(35)式によるSymplectic法の係数は ファイル symplectic.h に載せておく。ここで紹介した展開の仕方による係数には面白い性質があるので紹介して おこう。Symplectic法は短い時間 Δt の間の系の時間発展を 2種の時間推進演算子を交互に何回も作用して多ステップで計算するのだが、 1ステップでどれだけ時間が進むかをグラフにすると下図の様になる。 3つのグラフは下から(33)-(35)式の方式で 4次,6次,8次で展開した ものである。ステップごとに時間を進めたり戻しながら Δt の時間を 進むことがわかる。さらに、次数が上がるにつれて、この構造が自己相似的 に複雑化することもわかる。このため今まで紹介してきたこの分解方法は フラクタル分解と呼ばれる。
これら展開方法には多くの種類があり同じ次数でも精度や展開因子数が 異なる。必要な精度や速度に応じて選ぶ。
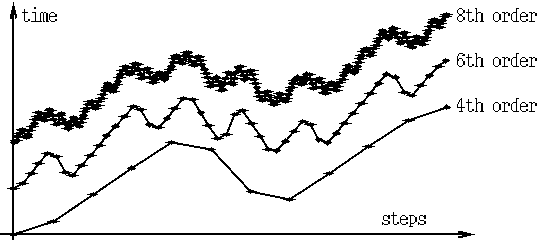
(33)-(35)式によるフラクタル分解
Symplectic法は古典力学のみならず量子論の計算においても威力を 発揮する。例えばSchrodinger方程式
において右辺の2項を分離すると、第1項のみなら自由粒子の 運動であり、第2項のみなら波動関数の位相が回転するだけである。 実際、第1項による時間発展の計算には多少の近似が必要だが 時間反転対称性を厳密に満たす計算が可能である。また流体力学の Navier-Stokes方程式
においても、右辺の2項を分離すると、第1項のみなら完全流体の運動であり、 第2項のみなら拡散方程式に還元できる。この方法もまた有用である。Symplectic法はさらに幅広く応用が効き、量子モンテカルロ法、経路積分、 分子動力学、量子化学、量子光学、加速器物理学、一般相対性理論、 カオスなど実にさまざまな分野で使われ始めている。
このSymplectic数値積分法は数値積分にも深遠なる理学があることを我々に 痛感させるものである。