流体力学は水や空気のような連続体の運動を解析する学問であるが、 その問題の多くは方程式が複雑なため、代数的な厳密解を得ることが できない。 そのため以前では、飛行機や自動車を設計する際にまわりの空気の流れの 様子を調べるには模型による風洞実験に頼るしかなかった。 しかし近年では、計算機の性能の飛躍的向上が大型計算機によるそれらの 流れのシミュレーションを可能にし、工学や気象の分野で著しい成果をあげる ようになった。 流体の計算手法にはさまざまな特殊な職人芸があり、それらはあまりに 専門的である。しかし流体の計算の基本的な部分には、すべての物理の 分野の計算に必要な大事な計算技術として、場の偏微分方程式の差分解法と 座標変換がある。 この章では、流体力学の典型的な問題である「円柱周りの2次元流れ」を 計算機で解くことにより、これらの技術を学ぼう。
流体の流れが十分遅い場合には、流体の密度の変化を無視することが できる。この場合、速さと長さの基準を適当にとることにより 流体の運動を支配する方程式に現れるパラメータは Reynolds number と 呼ばれるただ一つの定数 Re のみとなる。方程式は連続の方程式 (1)式とNavier-Stokes方程式(以降NS方程式と略す) (2)式である。
ここで v は流れの速度場、 p は圧力場を表す。Reynolds numberの具体的な値の導出は後回しにして、 まずこの2つの方程式をもう少し簡単な形に変形していこう。速度場 v に rot を作用させた場の量を渦度(vorticity)と 呼びωと表す。また、非圧縮のこのような速度場を生じる ベクトルポテンシャルを流れ関数(flow function)と呼びψと表す。 これらの定義を次式に示す。
速度と圧力についてのNS方程式(2)式をこの流れ関数と渦度を用いて 書き改めることができる。(2)式の両辺に rot を作用 させ、(1)式の関係を用いながらベクトル解析の種々の公式 を利用することで次の2つの式を得る。 かえって複雑になったが、この2つの方程式で未知の量ψ、 ωについて方程式系を完全に閉じることができる。3次元空間の流れでも、系の適当な対称性を仮定することにより 流れの本質を2次元空間の流れとして扱うことができる。 例えば、下図のような円柱の周りの流れは2次元流れとして 扱うことができると容易に想像できるであろう。
xy平面のみの流れ v=(v_x,v_y,0) を生じる流れ関数 ψとして次のものが考えられる。
2次元流れの典型的な例として円柱周りの流れを考えよう。 つまり、x軸正の方向から負の方向への一様な流れが、座標原点に 置かれた円形の障害物によってどう乱されるかを考える。
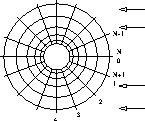
方程式(7)(8)式はデカルト座標で記述されているが 障害物が円形なので極座標に書き改めると便利である。 右図のメッシュのように円の表面近くを細かく、表面から 遠く離れた所は荒くメッシュする次の極座標系 (ξ,θ)系で考えることにする。
この方程式を解くためには初期条件と境界条件が必要である。 初期条件としては、v_x=-1,v_y=0の一様流となる ψ,ωを使う。すなわち、(12)式と (15)式より
となる。これは遠方(ξ=ξ_{far})での境界条件として そのまま使われる。 このように場の値そのものに課せられる境界条件を Dirichlet型境界条件と呼ぶ。他方、場の微係数の値に課せられる境界条件を Neumann型境界条件と呼ぶ。円の表面(ξ=0)での境界条件は、流体が粘性流体であることから 円の表面においては流れの速度は0である。 従って(12)式より ψは表面で一定値をとることがわかる。ψは定数項の自由度がまだあり、 そこで表面での値を0と定義しよう。 さらに (15)式式よりωの表面境界条件
を得る。ところが、ψ(ξ)を表面の近くでTaylor展開 して、ψ(0)=dψ(0)/ξ=0を考慮するとこの条件はより 簡単になる。結局、円の表面(ξ=0)での境界条件は次の通りである。方程式 (15)式は未知の場 ψ のLaplacianが 与えられた場ωを 満たすことを要請する方程式であり、このような形式の方程式を解くには 次の手段をとる。
(ξ,θ)平面上の格子点(i,j)でのψ(ξ,θ),ω(ξ,θ)の 値をψ_{i,j},ω_{i,j}と表して(15)式を差分方程式で 表してみよう。2階微分を2次精度で差分化すると次式となる。
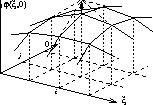
Δξ^2,Δθ^2はξ,θの差分間隔である。 これをψ_{i,j}についてまとめ直すと次式となる。 ψ(ξ,θ)が方程式(15)式9}や差分化表式 (21)式を満たしていなくても、格子点(i,j)について (21)式の右辺を計算してそれを左辺に代入すると その点に限り方程式を満たすことができる。この様子を右図に示す。 この作業を全格子点において実行するのである。 当然この修正で、こちらが立てばあちらが立たずの状況が起こるが この修正を何度も繰り返して実行すると全体がほどほどに 方程式を満たすようになる。このような手段を緩和法(relaxation method)と呼び、 ほどほどに方程式を満たすようになった 解をself consistent(自己無撞着)な解と呼ぶ。
必要な知識が揃ったので、プログラムを作り始めよう。ソースファイルは fluid.cc である。
XI_NUM は動径方向の格子点の数、 TH_NUM は角度方向の格子点の数を定義する。 場の量の1番目の添字がξ方向の要素のindexで、 2番目の添字がθ方向の要素のindexである。 前出のメッシュの図に付したように、周期境界条件に対応しやすい ようにindexを重複させている。 まず、exp(),sin(),cos()の関数の必要な 値と各格子点の位置 x,y をtableにしよう。#include "cip.h" #include "nxgraph.h" //---- definition of fundermental constants //---- experimental settings const double RE = 100.0; // Reynolds number const double IRE = 1.0/RE; // inverse of RE const double dT = 0.0625; // temporal step const int XI_NUM = 24; // radial cells const int TH_NUM = 48; // angular cells const double dXI = 0.125; // radial step const double dTH = 2*M_PI/(TH_NUM-2(; // angular step const double IdXI = 1.0/dXI; // inverse of dXI const double IdTH = 1.0/dTH; // inverse of dTH //---- index indicators const int XI_SUR = 0; // index of surface const int XI_FAR = XI_NUM-1; // index of farthest const int TH_STA = 1; // index of start angle const int TH_END = TH_NUM-2; // index of end angle //---- graphics settings const int WIN_WIDTH = 256; // width of window const int WIN_HEIGHT = 256; // height of window const int CYLINDER_R = 24; // radius of cylinder const double V_MAG = 16.0; // magnify factor of velocity //---- prototype of functions void InitFlow( void ); void SetBorder( void ); void ModifyPsi( void ); void UpdateOmg( void ); void DrawFlow( void ); //---- field variables double Psi[XI_NUM][TH_NUM]; // Flow Function field double Omg[XI_NUM][TH_NUM]; // Vorticity field
class ExpTable
{
double expo[4*XI_NUM];
public:
ExpTable( void ){
for( int i=-2*XI_NUM ; i<2*XI_NUM ; i++ ){
expo[2*XI_NUM+i] = exp( i*dXI );
}
}
inline double operator () ( int i ){
return( expo[2*XI_NUM+i] );
}
} Exp;
class SinTable
{
double sine[TH_NUM];
public:
SinTable( void ){
for( int j=TH_STA ; j<=TH_END ; j++ ){
sine[j] = sin( j*dTH );
}
}
inline double operator () ( int j ){
return( sine[j] );
}
} Sin;
class CosTable
{
double cosi[TH_NUM];
public:
CosTable( void ){
for( int j=TH_STA ; j<=TH_END ; j++ ){
cosi[j] = cos( j*dTH );
}
}
inline double operator () ( int j ){
return( cosi[j] );
}
} Cos;
class XTable
{
int x[XI_NUM][TH_NUM];
public:
XTable( void ){
for( int i=XI_SUR ; i<=XI_FAR ; i++ ){
for( int j=TH_STA ; j<=TH_END ; j++ ){
x[i][j] = WIN_WIDTH/2 + int(CYLINDER_R*Exp(i)*Cos(j));
}
}
}
inline int operator () ( int i, int j ){
return( x[i][j] );
}
} X;
class YTable
{
int y[XI_NUM][TH_NUM];
public:
YTable( void ){
for( int i=XI_SUR ; i<=XI_FAR ; i++ ){
for( int j=TH_STA ; j<=TH_END ; j++ ){
y[i][j] = WIN_HEIGHT/2 + int(CYLINDER_R*Exp(i)*Sin(j));
}
}
}
inline int operator () ( int i, int j ){
return( y[i][j] );
}
} Y;
//---- intialize flow as uniformal flow
void InitFlow( void )
{
for( int i=XI_SUR ; i<=XI_FAR ; i++ ){
for( int j=TH_STA ; j<=TH_END ; j++ ){
Psi[i][j] = -Exp(i)*Sin(j); Omg[i][j] = 0.0;
}
}
}
main() 関数はプログラムの大まかな流れを定める。
//---- main function
int main( void )
{
XEvent ev;
NXOpenWindow( "2D flow around a cylinder", WIN_WIDTH, WIN_HEIGHT );
NXEnable( NX_DOUBLEBUFFER );
InitFlow(); // inttialize flow as uniformal flow
do{ // evolution loop
SetBorder(); // set border condtions at surface and far away
ModifyPsi(); // solve phi by eq13
UpdateOmg(); // calculate next omg by eq10
DrawFlow(); // draw velocity filed
NXCheckEvent( NX_NOWAIT, ev );
}while( ev.type != KeyPress );
NXCloseWindow();
return(0);
}
//---- set border conditions on surface and far away
void SetBorder( void )
{
for( int j=TH_STA ; j<=TH_END ; j++ ){ // anguler loop
Psi[XI_SUR][j] = 0.0; Omg[XI_SUR][j] = (-2.0*IdXI*IdXI) * Psi[XI_SUR+1][j]; // surface
Psi[XI_FAR][j] = -Exp(XI_FAR)*Sin(j); Omg[XI_FAR][j] = 0.0; // far away
}
}
//---- derive flow function field (psi) from Laplace equation
void ModifyPsi( void )
{
int i, j, loop=8;
while( loop-- ){
for( i=XI_SUR+1 ; i<=XI_FAR-1 ; i++ ){ // radial loop
Psi[i][TH_STA-1] = Psi[i][TH_END]; Psi[i][TH_END+1] = Psi[i][TH_STA]; // cyclic condition
for( j=TH_STA ; j<=TH_END ; j++ ){ // anguler loop
Psi[i][j] = (0.5/(IdXI*IdXI+IdTH*IdTH))*(
+ (IdXI*IdXI)*(Psi[i+1][j]+Psi[i-1][j]) + (IdTH*IdTH)*(Psi[i][j+1]+Psi[i][j-1]) + Exp(2*i)*Omg[i][j] );
}
}
}
}
//---- update vorticity field (omg)
void UpdateOmg( void )
{
int i, j;
for( i=XI_SUR+1 ; i<=XI_FAR-1 ; i++ ){ // radial loop
Omg[i][TH_STA-1] = Omg[i][TH_END]; // cyclic condition
Omg[i][TH_END+1] = Omg[i][TH_STA];
for( j=TH_STA ; j<=TH_END ; j++ ){ // anguler loop
Omg[i][j] +=
dT*Exp(-2*i)*( + (IdXI*0.5) * (Psi[i+1][j]-Psi[i-1][j]) * (IdTH*0.5) * (Omg[i][j+1]-Omg[i][j-1])
- (IdTH*0.5) * (Psi[i][j+1]-Psi[i][j-1]) * (IdXI*0.5) * (Omg[i+1][j]-Omg[i-1][j]) )
+ dT*Exp(-2*i)*IRE*( + (IdXI*IdXI) * (Omg[i+1][j]-2*Omg[i][j]+Omg[i-1][j])
+ (IdTH*IdTH) * (Omg[i][j+1]-2*Omg[i][j]+Omg[i][j-1]) );
}
}
}
//---- derive velocity field and draw them
void DrawFlow( void )
{
int i, j;
double Vxi, Vth, Vx, Vy;
NXClearWindow();
for( i=XI_SUR+1 ; i<=XI_FAR-1 ; i++ ){ // radial loop
for( j=TH_STA ; j<=TH_END ; j++ ){ // anguler loop
Vxi = (+0.5*IdTH) * Exp(-i)*(Psi[i][j+1]-Psi[i][j-1]);
Vth = (-0.5*IdXI) * Exp(-i)*(Psi[i+1][j]-Psi[i-1][j]);
Vx = Vxi*Cos(j) - Vth*Sin(j);
Vy = Vxi*Sin(j) + Vth*Cos(j);
NXDrawMoveto( X(i,j), Y(i,j) );
NXDrawLinerel( int(V_MAG*Vx), int(V_MAG*Vy) );
}
}
NXFlush();
}
 |
Reynolds number が100程度の流れでは、流れ始めには円形の障害物の 後方に対称(プログラムが描く図では上下対称)な2つの渦が生じる。しかし この渦の対称性は不安定ですぐにどちからの渦が優位になる。この対称性の 自発的な破れの原因はNS方程式の粘性項により対称な状態が不安定な状態と なったためである。
時間を追って眺めると、渦は流れと共に後方へ流れ去り、代わって 円の表面の先の渦とは上下逆の位置に新たな渦が生じる。それが成長して、 後方へ流れていく。そしてまた次の渦が上下逆の位置に 生じる。このようにしてできる渦の上下の列はカルマン渦列 (Karman street of alternating vortices)と呼ばれ、 日常の身近な所にも現れる物理現象でもある。
流体計算などの偏微分方程式を数値解析する際には、その計算の安定性が 致命的な問題となっている。 先の円柱周りの流れのプログラムで、Reynolds numberを200とすると どうなるであろうか。流れは信じられない程の激しい流れとなり、 遂にはプログラムはエラーとなって強制終了する。
このような数値解の不安定性の原因は、用いた差分解法のアルゴリズム そのものにあり、メッシュを細かくしても不安定性を克服できない。 そのため多くの研究により安定なアルゴリズムが開発され、多大な成功が 修められている。この技術については流体力学の専門書を参照されたい。
一般論として、偏微分方程式の差分解法の安定性をチェックするための 方法であるvon Noumannの安定解析を紹介しておこう。 チェックする対象として次の1次元拡散方程式 とその差分化表式を取り上げる。
ここで j は空間のindexであり、n は時間のindexである。Fourier変換で得られる波数成分のひとつに注目しよう。 この成分 u_j^n は次の形式で表される。
つまり、時間依存因子はある複素数 ξ の n 乗となる。 |ξ|>1ならばこの成分は時間と共に増大し、解を壊す要因となる。従って |ξ|≦1であることが差分方程式が安定であることの必要条件である ことがわかる。(24)式を(23)式 に代入して整理するとξの値が得られる。 これが任意の k について |ξ|≦1であるためには であることが必要十分条件である。この条件が満たされるように 時間と空間を差分化することが、(23)式の 差分化表式で安定な計算を行うための必要条件である。 (23)式の差分化の様に、uの現在での値からすぐに 次の時間での 値が計算できる差分化を陽的(explicit)な差分化と呼ぶ。explicitな 差分化は計算が簡単であるが計算結果の安定性にはさまざまな条件が つき、安定性はあまり良くない。これに対して次のような差分化を陰的(implicit)な差分化と呼ぶ。
これに対しても(24)式を代入して von Noumannの安定解析を行ってみよう。ξは となり、これは任意の k について |ξ|≦1の無条件安定である。 つまりこの例の方程式では陰的な差分化を行えば、発散しない解が 得られる。精度を上げるためにはもちろん差分間隔を小さくする。なお、(27)式で u_j^{n+1} を計算するためには、 すべての j の u_j^{n+1} に関する(27)式の 連立方程式を解く計算を行うか、緩和法を用いる。
偏微分方程式の差分解法は非常に奥が深いので、興味のある読者には 専門書を参照されることを勧める。 本書で強調しておくことは、計算機を安易に信じて単純に計算を行うことの 危険性と、その危険性を回避するための人間の英知と努力があることである。