Youngの干渉実験でお馴染みのように光の波動性は干渉として物理的に明確と なる。干渉現象も含めて光の伝搬の様子を光の波動性から数学的に導く手法が 波動光学である。後で解説するように光の干渉とFourier変換には密接な関連 がある。本節では光の干渉を計算機で再現することを通じて、Fourier変換の 意味を理解することを目指そう。
一本の光路を走る波長λの光の波動関数 f を光路上の距離 l と 時刻 t によって次のように表す。
ここでφは定数の位相のずれである。観測にかかる物理量は|f|^2の 光の強度なので、物理的にはこの位相のずれφは任意の値をとることが できる。ある時刻 t で 2π ft = φ となるようにφをとれば、 結局波動関数から時間依存が除かれる。フィルムに垂直に平面波を入射して、このフィルムの模様がその先の スクリーンにどのように写るかを考えよう。 下図に座標系と記号の定義を載せる。
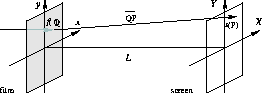
フィルムが非常に小さいならば、(5)式中の x^2+y^2 による位相の変化も無視でき簡単な次式となる。
これがFraunhofer回折の公式である。この積分の中身は f(x,y)のFourier変換であることに注目しよう。 スクリーン上で観測される光の強度 |s(X,Y)|^2 は となる。光の回折による干渉像がFourier変換で表されることがわかった。 これで計算機で光の干渉を計算できる。しかし、この変換はFourier変換の絶対値の2乗であり、位相情報が失われて いる。そのため、逆Fourier変換を使っても元に戻すことはできない。 つまりスクリーンを写真乾版として、このような干渉像を撮影したものから、 元の像を一意に特定することはできないのである。
干渉像を撮影したフィルムから元の像を得る技術がholographyである。 最も単純な種類のholographyについて簡単にその原理を解説しよう。
フィルム上での波動関数 f とL離れたスクリーン上の波動関数 s を s = F_L(f)と結びつける汎関数 F_L() をpropagatorと呼ぶ。 ところで、フィルムに当てた光と同じ光をフィルムを通さずに直接 スクリーンに当ててみよう。この光のスクリーン上での 波動関数は1としても物理的観測には変わり無い。 スクリーン上の波動関数 s'は
となる。これを撮影して、透過率 H=|s'|^2 なるフィルムを 作ることが技術的に可能である。Hを展開すると、 となり、この後ろの2項に位相情報が残されている。 このフィルムに同じ平面波を直接当てた時のスクリーン像 F_L(H) は次の様になる。Hの第4項による像は F_L^* が F_L の逆変換 になる性質があるので、 となり、見事に元の像 f がスクリーン上に得られる。Hの第3項による像は となり、これはあたかもスクリーンの手前2Lつまりフィルム後方Lの所 から元の像の光が伝わってきたかのような光である。つまりスクリーンの 位置でフィルムを眺めるとその向こうに像があるかのように見えるのである。 これがholographyである。Hの第2項による像は中心に明るい点を作るだけである。最後に、H()の第1項に よる像は明確な像とはならず、ただ全体の暗い背景となるだけである。
propagatorとして単純なFourier変換を採用して holographyの現象を計算機で再現することができる。
実際にFourier変換を計算して光の干渉をシミュレーションしてみよう。 1次元の関数 f(x) のFourier変換 F(X) を次式で定義する。 Fourier変換には色々な定義の仕方があることに注意しておこう。
単なる積分と思われるかもしれないが、単純にこれを計算すると 計算機にとってかなりの重労働となる。Fourier変換は大事な計算なので これを効率良く計算する方法を学んでおこう。関数 f(x) について与えられる情報が離散的な格子点 x=jΔx (j=0,…,N-1) での値のみであるとしよう。 Fourier変換 F(X) にはあらゆる波が含まれ得るが、 下図の実線で描いた波は、格子点でのその値を見る限りでは 破線で描いた波と同じである。これは破線の波が実線の波にとって 代わることができることを意味している。
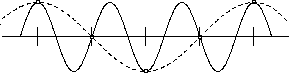
f(x)の情報がN点しか与えられていないので、F(X)の自由度は N でしかありえない。従って X を|X| ≦ 1/2Δx の範囲で N等分した格子点、すなわち、X=k/NΔx (k=-N/2,…,+N/2) での F(X) の値を考えるのが適当と思われる。 ただしNは偶数とした。k=-N/2の波とk=+N/2の波は同じなので 確かに自由度は N個である。
(12)式は次の通りとなる。
これを離散Fourier変換と呼ぶ。(13)式は各 k について N個の格子点での計算が 必要なので全部のkについて合計 N^2回の計算が必要に思われるが、実は 高速Fourier変換(Fast Fourier Transform(FFT))と呼ばれるアルゴリズム があり、この方法では N log_2{N} のオーダーの計算量で済む。 単純な比較は危険だが、N=256でのN^2とN log_2{N}の差は歴然である。
このFFTのアルゴリズムを簡単に紹介しよう。 FFTでは系のサイズ、つまり格子点の個数 N が例えば256=2^8のように 2の巾乗となる場合にもっとも威力を発揮する。なのでNをそのような 値にとることにしよう。
(13)式のjの和について、jが偶数の項と奇数の 項で別々に和をとるように変形する。
サイズNのFourier変換(13)式がサイズN/2の2本の Fourier変換に位相をかけた和になることがわかる。 さらに同様に偶数項と奇数項のそれぞれを4で割った余りに基づいて 和を分割すれば、サイズN/4の4本のFourier変換に位相をかけた和になる。この論法をさらに繰り返すと最終的にはサイズ1のN本のFourier変換に 位相をかけた和になる。サイズ1のFourier変換とは恒等変換であるから、 ここから逆に分解を遡って位相をかけて足し合わせる作業を進めていくと Fourier変換になるのである。 N=8の簡単な場合についてそのF_0とF_1のこの分解による表現を記しておく。
さらに計算の流れの模式図を下図に載せる。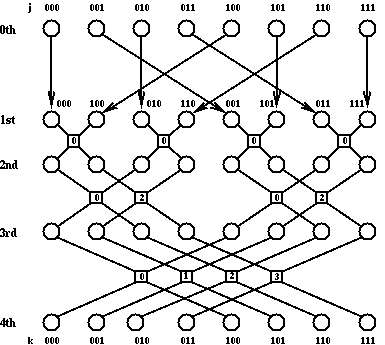
以後、位相をかけて和をとる操作が3段階続く。[n] の交差する操作は 上の2項のうち右上の項にexp[-2π i n/8]をかけて、 左上の項に足したものを左下の項へ、 左上の項からこれを引いたものを右下の項へ設定することを表す。
このアルゴリズムをプログラムで表現するのはやや複雑であるが 以下のようになる。 まず、指数関数exp()とindexのビット反転のtableを用意する。
class RevTable
{
int reve[N];
public:
RevTable( void ){
for( int i=0 ; i<N ; i++ ){
int rev=0;
for( u_int mask1=1, mask2=N/2 ; mask2 ; mask1<<=1, mask2>>=1 ){
if( i&mask1 ) rev|=mask2;
}
reve[i] = rev;
}
}
inline int operator [] ( int i ){
return( reve[i] );
}
} Rev;
class ExpTable
{
Complex expo[2*N];
public:
ExpTable( void ){
for( int p=-N+1 ; p<=N-1 ; p++ ){
expo[p+N] = Complex( cos(2*M_PI/N*p), sin(2*M_PI/N*p) );
}
}
inline Complex operator [] ( int p ){
return( expo[p+N] );
}
} Exp;
//---- 1-Dimensional Fast Fourier Transform
void FFT1( int sign, Complex src[N], Complex dst[N] )
{
int k;
// copy from source array at reversed index to destination array
for( int j=0 ; j<N ; j++ ) dst[Rev[j]] = src[j];
// Uncomment below lines, and x=0, k=0 are treated as the center of the arrays.
/**********************
for( k=N/2 ; k<N ; k++ ) dst[k] *= -1.0;
**********************/
// Danielson-Lanczos's algorithm
int k0, k1, k2, dk, p, dp;
Complex ex, work;
for( dk=0x01, dp=HALF_N ; dp ; dk<<=1, dp>>=1 ){
for( k0=0, p=0 ; k0<dk ; k0++, p+=sign*dp ){
for( k1=k0, ex=Exp[p] ; k1<N ; k1=k2+dk ){
k2=k1+dk;
work = dst[k2] * ex;
dst[k2] = dst[k1] - work;
dst[k1] += work;
}
}
}
// Uncomment below lines, and x=0, k=0 are treated as the center of the arrays.
/**********************
for( k=1 ; k<N ; k+=2 ) dst[k] *= -1.0;
**********************/
}
波数の配列への格納の仕方に注意がいる。波数の配列のindex と (13)式の波数kの対応関係を以下に記す。
| index | 0 | 1 | … | N/2 | … | N-2 | N-1 |
| k | 0 | +1 | … | +N/2,,-N/2 | … | -2 | -1 |
| index | 0 | 1 | … | N/2 | … | N-2 | N-1 |
| k | -N/2 | 1-N/2 | … | 0 | … | N/2-2 | N/2-1 |
サイズ N times Nの2次元のFFTは x軸方向のN本の1次元FFTを行ってから、 y軸方向のN本の1次元FFTを行うので、複素数の演算回数は合計
となり計算量はサイズ N のオーダー N^2 log_2{N}であることがわかる。以下に2次元FFTの FFT2() 関数を載せる。ループを効率化させる ためにx軸方向の変換とy軸方向の変換をまとめて行う。 ただし、この関数は正逆両方の変換において 1/Nの係数をかける。
//---- 2-Dimensional Fast Fourier Transform
void FFT2( int sign, Complex src[N][N], Complex dst[N][N] )
{
int kx, ky;
// copy from source array at reversed index to destination array
for( int jx=0 ; jx<N ; jx++ ){
for( int jy=0 ; jy<N ; jy++ ){
dst[Rev[jx]][Rev[jy]] = (1.0/N)*src[jx][jy];
}
}
// Uncomment below lines, and x=0, k=0 are treated as the center of the arrays.
/**********************
for( kx=N/2 ; kx<N ; kx++ ){
for( ky=0 ; ky<N/2 ; ky++ ){
dst[kx][ky] *= -1.0; dst[ky][kx] *= -1.0;
}
}
**********************/
// Danielson-Lanczos's algorithm
int k0, k1, k2, dk, p, dp;
Complex ex, work;
for( dk=0x01, dp=HALF_N ; dp ; dk<<=1, dp>>=1 ){
for( k0=0, p=0 ; k0<dk ; k0++, p+=sign*dp ){
for( k1=k0, ex=Exp[p] ; k1<N ; k1=k2+dk ){
for( ky=0, k2=k1+dk ; ky<N ; ky++ ){ // transform columns
work = dst[k2][ky] * ex;
dst[k2][ky] = dst[k1][ky] - work;
dst[k1][ky] += work;
}
for( kx=0, k2=k1+dk ; kx<N ; kx++ ){ // transform rows
work = dst[kx][k2] * ex;
dst[kx][k2] = dst[kx][k1] - work;
dst[kx][k1] += work;
}
}
}
}
// Uncomment below lines, and x=0, k=0 are treated as the center of the arrays.
/**********************
for( kx=0 ; kx<N ; kx++ ){
for( ky=kx+1 ; ky<N ; ky+=2 ){
dst[kx][ky] *= -1.0; dst[ky][kx] *= -1.0;
}
}
**********************/
}
畳み込み演算(convolution)と呼ばれるFourier変換特有の演算がある。 これは大事な法則を含むので学んでおこう。畳み込みの演算子 * の 演算規則は次式で定義される。
すると、このf(x) * g(x)のFourier変換 F は次のようになる。 つまり、2関数の畳み込みのFourier変換はそれぞれのFourier変換の 積となることがわかる。g(x)として、間隔aの点列を表す関数 Σ_n δ(x-na) を 用いると、f(x) * g(x)は次のようになる。
f(x)が狭い範囲のみに値をもつ関数とすると、これは間隔aでそのf(x) の関数形が並んだものを表す。つまり小図形の繰り返し構造を表す。 これのFourier変換は となり、波数空間で間隔 1/a で点列が並び、その明るさがF(X) で変化する ことになる。以降のFourier変換の実例でこの状況を見てみよう。実践は簡単なのでプログラムの詳細は紹介せずに基本的な3つの例を 紹介する。計算する画像の大きさは256 times 256で、画像形式は 256階調の greyscaleのPGM形式(raw)である。
小さな穴による光の回折をFraunhofer回折の式 5()式 で計算する。プログラムソースは fraunhofer.cc である。
下図のように四角形、円形の開口があるフィルムに よる干渉模様を計算すると、それぞれ下図になる。
開口の部分で f(Q)=1 で、他でf(Q)=0として、Fourier変換を 代数的に計算すると、四角形の開口は
の形状となり、円形の開口は1次のBessel関数J_1(R)を用いて の形状となる。 ただし円形の開口は計算機内ではギザギザなのでその効果が出ている。代数的な予測とこの干渉模様の実測とを比較することにより、 元の開口の形状を非常に正確に知ることができる。




先の例と同じ形をした開口が格子状に並んだ右図のフィルム よる干渉模様を計算すると、それぞれ下図になる。
どちらも点が格子状に並ぶ。これは繰り返し構造をもった 開口の特徴でもある。干渉像の点格子の間隔は元の格子の間隔の 逆数に比例する。
格子がところどころで欠落している。 これは点格子と小図形の畳み込みのFourier変換の結果である。 先の開口ひとつの干渉模様と比較すると確かにこれが点格子の 明るさの因子となることがわかる。
この明るさの変化から元の格子ひとつの形状を知ることができる。


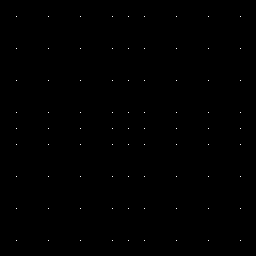

もっとも単純な原理による簡単な像のholographyを載せる。 propagatorには単純なFourier変換 (12)式を用いる。 ソースファイル名は holography.cc である。
 元の像 |
 holographyに撮影された像 |
 再現された像 |
Fourier変換のデータ処理における重要性は色々あるが、ひとつに、繰り返し 構造をもつ像の特徴が極めて明確になり精密な分析が可能になることである。 ふたつに、繰り返し構造をもたないノイズを識別することが容易になり、 データからノイズを除去できることである。 このため、電子顕微鏡によるタンパク質分析や、X線,電子線による結晶表面解 析などで実際に活用されている。近年では電子線を用いたholographyによる 結晶解析の研究も盛んで、結晶試料の干渉像から結晶の構造が直ちに判明でき るようになりつつある。
また、偏微分方程式の解析にもFourier変換は使われる。 実空間で方程式を解くより、波数空間で解く方が安定性や精度の面で 優れる場合がある。高Reynolds numberでの流体 footnote{系の対称性が必要で、工学の設計ではあまり使われない。} や物質内部の電子状態 footnote{最近は実空間でより良く解く研究が盛んである。} の計算などがある。
本節で示したように、Fourier変換の本質は目に見えて楽しい光の干渉現象 から理解することができるのである。例に載せた像以外にも各自さまざまな 像の干渉を計算して、Fourier変換の性質の理解を深めてほしい。