★ 古典力学の問題

● 非線形力学

■ 非線形の点列漸化式のカオス

微分方程式に非線形な項 (x^2など) が含まれると大抵の 方程式は解析的には解けなくなる。それでも計算機は数値積分により なんとかその方程式の数値的な近似解を導き出す。

点列の漸化式も非線形な項が含まれると点の一般解は得られなくなる。 それでも計算機は漸化式を簡単に計算することができるので 点の系列を追うことができる。これにより非線形項のもたらす 驚くべき効果を我々は知ることになる。

2次元平面内の点の座標の系列 (x_n,y_n) が次の 非線形項を含む漸化式で与えられているとしよう。

(1)

(2)

#include "cip.h"
#include "nxgraph.h"

const int WIN_WIDTH  = 256;
const int WIN_HEIGHT = 256;

int main(void)
{
  const double a = -1.57, b = 0.96, c= -4.00, d = 5.0;
  double x = 1.0, y = 0.0, ox;

  NXOpenWindow("Chaos", WIN_WIDTH, WIN_HEIGHT );

  for( int n=0 ; n<4096 ; n++ ){
    NXDrawPoint( (int)(8*x)+WIN_WIDTH/2, (int)(8*y)+WIN_HEIGHT/2 );
    ox = x;
    x  = a*x + b*y + c + d/(1.0+x*x);
    y  = -ox;
  }

  XEvent ev;
  NXCheckEvent( NX_WAIT, ev );
  NXCloseWindow();

  return(0);
}

このプログラムが描く非線形漸化式のカオス

点列は計算したらすぐ描くので過去の点の座標を保存する 必要は無い。なので昔の値に上書きしながら次の点に進む。 ただし、y を更新する際に用いる x を正しく昔の値を使うことに 注意しよう。点の座標をそのまま画面に描くと分布の範囲が小さすぎたり 画面からはみ出てしまうので適当に拡大と平行移動をしてから点を 描く関数 NXDrawPoint() を呼び出す。

このプログラムが描く点の分布は右上の図の通りである。漸化式 (1)(2)からは想像できない程の複雑で奇妙な絵になる。この図は カオス(chaos)と呼ばれる一般的な現象の性質を良く表したほんの一例である。 なぜこのような図形になるのか、パラメータを変更するとどうなるのか、 初期値と第 n 点の関係や全体の関係はとどうなっているか、 各自でいろいろ試してカオスについての見解を得てほしい。

■ Mandelbrot図形

下に載せたMandelbrot(マンデルブロ)図形はB.B.Mandelbrotが発見した 複素平面上での図形である。この図形の描画規則は単純である。 ある複素数のパラメータ A について、複素平面の点列の漸化式

(3)

この計算操作は現在のコンピュータなら簡単に行える。 ソースファイルは mandel.cc である。

#include "cip.h"
#include "complex.h"
#include "nxgraph.h"

const int WIN_WIDTH  = 256;
const int WIN_HEIGHT = 256;
const double MAG     = 1.0/128.0;

//---- main function
int main( void )
{
  const Complex Ao( -0.5, 0.0 );
  Complex A, Z;
  int n;

  NXOpenWindow("Mandelbrot", WIN_WIDTH, WIN_HEIGHT );

  for( int ay=0 ; ay<WIN_HEIGHT ; ay++ ){
    for( int ax=0 ; ax<WIN_WIDTH ; ax++ ){
      A = Ao + mag*Complex( ax-WIN_WIDTH/2, ay-WIN_HEIGHT/2 );
      Z = Complex( 0.0, 0.0 );
      for( n=0 ; abs2(Z)<4.0 && n<256 ; n++ ){
        Z = Z*Z + A;
      }
      NXSetColor( n );
      NXDrawPoint( ax, ay );
    }
  }

  XEvent ev;
  NXCheckEvent( NX_WAIT, ev );
  NXCloseWindow();

  return(0);
}

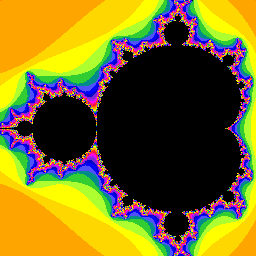
このプログラムが描くMandelbrot図形

外側2つの ax,ay に関するループは整数の window 座標を window 内で 操引きさせる。毎回その座標に対応するパラメータ A の値を計算する。 内側の n に関するループは漸化式を追って次々に新しい点の値を元の 変数に上書きする Z^2>4 となるか256ステップを越えたらループを終え、 その時の n の値に応じた色で座標 ax,ay に点を描く

この図形の持つ意味は図形を拡大すると明らかになる。各自試してみよう。 拡大するたびに、この図形は複雑なさまざまな美しい姿を見せてくれる。 そして重要なことは、ある部分にはMandelbrot図形の最初の図の形と 相似で非常に小さい形のMandelbrot図形自身があることである。 Mandelbrot図形は自己相似の特徴を持っているのである。それゆえ この図形はfractal(フラクタル)の1種である。 Mandelbrot図形の漸化式は非線形なので点列の振舞いはchaoticである。 パラメータ A がわずかでも異なれば点列の振舞いは全く異なり、 描かれる色も異なる。それゆえ無限に細かい構造ができるのである。 Mandelbrot図形はchaosの点列の結果の集合なのである。 それがfractalの性質を持つことには数理現象の奥深さが感じられる。