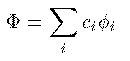 (01)
(01)量子論を化学に応用してみると、それまで不可解であったさまざまな現象に
説明を付けることできる。それと共に、量子論という微視的、非感覚的
な理論を身近に感じとることができる。
分子の電子の状態を量子論的に計算することは一般には大計算であるが、
1931年にE.Huckel が考案したHuckel 近似を用いると、その大雑把な
近似にも関わらず、分子の電子状態の定性的振舞を比較的簡単に
知ることができる。
本節では、簡単な有機化合物にHuckel 近似を適応して、
それが示す定性的性質を考えてみる。
分子中の1電子の波動関数 Φ は、各原子のあらゆる原子軌道の波動関数 Φ_i を基底関数とした線形結合で表される。
Hamiltonai H での全エネルギーの期待値 E は次式から得られる。 これに (1)式 を代入して整理すると、 ここで、 S_{ij} は原子軌道の重なり積分、 H_{ij} はHamiltonaiの行列要素であり、次式で定義される。 全電子のエネルギーの和が最小になるのが基底状態であるが、 それとは異なり、1電子のエネルギーが最小になる条件を探そう。 (3)式を \delta E=0 のもとで \delta c_j^\ast で変分 すると簡単な次式を得る。 係数 c_i をベクトルと見て、 H_ij - E S_ij を行列と見れば、 これが行列の固有値問題であることは明らかであろう。 この固有値をエネルギーの低い方から選んで、それらを分子の全部の電子の エネルギーと分子軌道関数とみなすのがHuckel 近似である。実際には、もちろん電子間相互作用のため、各電子のエネルギーが 最小になることが 基底状態の条件ではないし、電子の数が変わればHamiltonianも変わるので、 \Huckel 近似は非常に大雑把な近似である。また、1式のように 展開するには無限個の基底関数が必要であるが計算では有限個しか扱えない (それでも数千の基底関数を用いることもある。)。 しかしながら、\Huckel 近似による計算結果には 分子の量子論的定性的性質がはっきり現れ、実験でもその性質は確かめられている。
下図に示した平面的な分子構造を持つトランス・ブタジエンを例に
分子軌道を考えよう。基底関数として、各水素原子の 1S と、
各炭素原子の 1S,2S,2Px,2Py,2Pz だけを使い、
この線形結合で近似的に分子軌道を表すことにする。
分子面に垂直に炭素の 2Pz 軌道をとると、他の軌道はこの分子面に対して
対称となる。ところが炭素の 2Pz 軌道だけは分子面に対して反対称である。
このため、 2Pz 軌道と他の軌道との間の H_ij,S_ij は 0 になる。
このことは (6)式の行列の内部が 2Pz 軌道に
関する部分の小行列と他の軌道に関する部分の小行列の2つのブロックに分
けられることを意味する。従って、固有値の計算も別々に行うことができる。
そこで 2Pz 軌道だけで構成される π 電子の分子軌道を求めてみよう。
この例では4つの炭素原子に属する計4つの 2Pz 軌道が基底関数である。 同じ軌道同士では S_jj=1 である。また、 H_{jj}≡ E_o と表そう。 近似として、隣接軌道同士では S_ij= S, H_ij= H とすべて 一定値とし、それ以外の軌道間では、 S_ij= 0, H_ij= 0 としよう。 (6)式を具体的に書き下す。
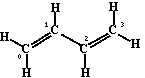
トランス・ブタジエンの分子構造
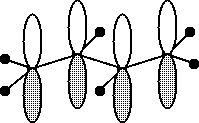
2Pz 原子軌道による π 分子軌道
Huckel 近似を用いて、さまざまな分子の π 分子軌道を計算する
プログラムを作ろう。ソースファイル名は huckel.cc である。
計算の要は対称行列の固有値を計算することにあるが、
本書では対称行列の固有値と固有関数を求める関数 Jacobi() を
提供して、これをブラックボックスとして使うことにする。
なので、プログラムについてここで解説することはあまり無い。
だが、2次元配列を扱いやすくするために class Array2d を設計
することと、 main() 関数での作業の流れと、計算結果の
表示について解説する。
まず、任意次元の正方行列を関数間で受渡しできるようにするための 機構 class Array2d を設計しよう。
//---- declaration of class Array2d
class Array2d
{
int dim; // dimension of this array
double* head; // pointer to the head of this array
double** array; // pointers to the head of each rows
public:
Array2d( int _dim );
~Array2d();
double* operator [] ( int i );
int Dim( void );
void SetZero( void );
void SetUnit( void );
void Print( void );
};
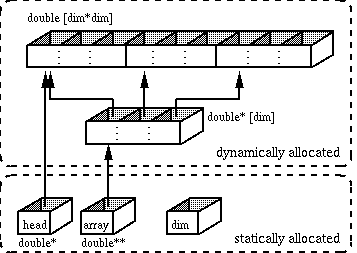
2次元配列のアドレスの管理の仕方
Constructorで行列の次元を指定できるようにしよう。
ここで行列要素のためのメモリを動的に確保して、その先頭アドレスを
head に格納する。次に各行の先頭アドレスを
格納するためのポインタ配列変数のためのメモリを動的に確保し、
その先頭アドレスを array に格納する。最後にその
ポインタ配列変数の各要素に各行の先頭アドレスを格納する。
Destructorは確保したメモリを解放する。
//---- constructor, allocates memory and set pointers
Array2d::Array2d( int _dim )
{
dim = _dim;
head = new (double) [dim*dim];
array = new (double*) [dim];
for( int i=0 ; i<dim ; i++ ) array[i] = &head[i*dim];
}
//---- destructor, free the memory
Array2d::~Array2d()
{
delete [] head; delete [] array;
}
//---- represents head address of each rows
inline double* Array2d::operator [] ( int i ){
return( array[i] );
}
//---- represent dimension of this array
inline int Array2d::Dim( void ){
return( dim );
}
main() 関数を見てプログラムの流れを理解しよう。
//---- main function
int main( void )
{
const int ORBITS = 4;
Array2d A(ORBITS), V(ORBITS);
A.SetZero();
A[0][1] = A[1][0] = 1.0; A[1][2] = A[2][1] = 1.0; A[2][3] = A[3][2] = 1.0;
Jacobi( A, V );
A.Print();
V.Print();
const int WIN_WIDTH = 24 + (ORBITS-1)*28 + 16 + 76;
const int WIN_HEIGHT = 32 + (ORBITS-1)*64 + 32;
NXOpenWindow( "Huckel approximation", WIN_WIDTH, WIN_HEIGHT );
Draw( A, V );
XEvent ev;
NXCheckEvent( NX_WAIT, ev );
NXCloseWindow();
return(0);
}
DrawPz() 関数は画面の指定された位置に 2Pz 軌道を表すアレイ型を
描く。原子軌道の分子軌道への寄与を大雑把に表すためだけの目的なので
描き方は極めて単純である。
Draw() 関数は DrawPz() 関数を呼び出して
各固有ベクトルに対応した分子軌道の様子を横一列に描く。
//---- draws pz orbital with given magnitude at given position
void DrawPz( int x, int y, double c )
{
int r;
if( c>0.0 ){
r = int(c*24.0);
NXSetColor( NX_PINK ); NXFillCircle( x, y-r, r );
NXSetColor( NX_CYAN ); NXFillCircle( x, y+r, r );
}else{
r = int(-c*24.0);
NXSetColor( NX_CYAN ); NXFillCircle( x, y-r, r );
NXSetColor( NX_PINK ); NXFillCircle( x, y+r, r );
}
}
//---- draws orbitals
void Draw( Array2d& A, Array2d& V )
{
int i,j;
NXClearWindow();
for( j=0 ; j<V.Dim() ; j++ ){
for( i=0 ; i<V.Dim() ; i++ ){
DrawPz( i*28+24, j*64+32, V[i][j] );
}
NXSetColor( NX_WHITE );
NXDrawPrintf( 4, j*64+36, "%d", V.Dim()-j-1 );
NXDrawPrintf( i*28+16, j*64+36, "X = %+6.4lf", A[j][j] );
}
NXFlush();
}
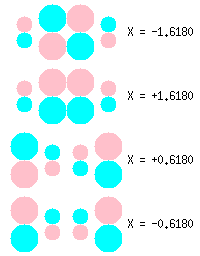
ブタジエンの π 分子軌道
ブタジエンでの結果を検討しよう。
表示される固有値 X が大きい程、軌道エネルギーは低い。
エネルギーの高い軌道ほど 2Pz 軌道の係数の正負の反転が頻繁、
つまり波動関数に節が多くあることがわかる。
各炭素原子の 2Pz 原子軌道には 1個の電子があるので、
この π 分子軌道には4個の電子が関係する。
各分子軌道にはスピン自由度のため2個の電子が入ることができ、エネルギー
の低い分子軌道から電子が入るので、2つの軌道が完全に占拠される。
従って図の下から2番目の分子軌道が
HOMO(Highest Occupied Molecular Orbital)、3番目の分子軌道がLUMO
(Loweset Unoccupied Molecular Orbital)である。
HOMO、LUMO共に炭素鎖の両端において波動関数の絶対値が大きくなって いる。そのため、付加重合反応が起こり易い所は、電子気陰性度の高い置換 基でも低い置換基でも、この炭素鎖の両端なのである。
シス・ブタジエンとエチレンとの重合反応である Diels-Alder 反応 のような π 分子軌道同士の結合は、双方のHOMEの電子が 他方のLUMOに流れることによってなされる。エチレンの π 分子軌道も Huckel 近似で簡単に求まり、その結果、下図のように シス・ブタジエンのHOMOとエチレンのLUMO、 シス・ブタジエンのLUMOとエチレンのHOMOの波動関数の符合が共に 合っていているので、合体し易いことがわかる。
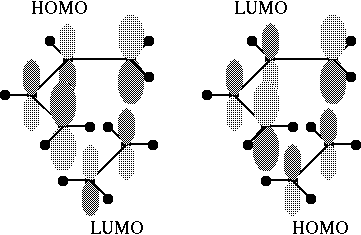
Diels-Alder 反応
このように分子の反応を決定する要因の根本は電子密度ではなく、 波動関数そのものであることがわかる。量子力学が分子の世界に 大きな影響力を持っているのである。
作成したプログラムはより複雑な分子の π 分子軌道の計算もできる。 さまざまな分子について計算してみて、その計算値から予測される 分子の性質が、実験的事実と整合するかどうか調べてみよ。