 |
÷
Japanese version is available.
Last updated, Jan 27, 2003.
The purpose of our study is to establish a standard computational method for large-scale and long-term fisrt-principles numerical simulations of time-evolving quantum electronic states. The base equation for this study is the time-dependent Schroedinger equation. In principle, by solving this partial differential equation numerically, it would be possible to analyze many kinds of quantum dynamic phenomena. However it is not straightforward. Many researchers have developed efficient numerical methods, but still there are some rooms for further improvements.
In the numerical simulation, the norm of the time-evolving wave function should be preserved. It is the most significant requirement for the simulation. Otherwise, eventually, the norm increases explosively or decreases to zero, and it can not give physically meaningful results. The norm is preserved only if the time evolution operator is exactly unitary. We have developed a numerical method which ensures exact unitarity.
A wave function is usually expressed by a linear combination of plane waves. This expression needs the Fourier-transform to calculate the matrix elements of the Hamiltonian many times. However, we utilize another expression by real space grid points. In this expression, the Hamiltonian is represented by a very sparse matrix. We have developed a method for the TD-Schroedinger equation by utilizing several computational techniques. One of the techniques is the exponential product method which has been widely used in many kind of computational simulations. We found the use of the Cayley's form implemented by FEM is very effective, and formulated a new method which can handle many kinds of systems under an electric field and magnetic field.
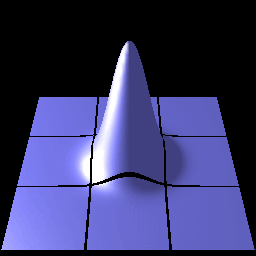
Figure 1 shows the result of a simple simulation using our method. Please move your mouse pointer inside the image. This animation demonstrates the flow of electron wave packets through a quantum wire on a 2D system.
|
|
÷
Cayley's form is a kind of implicit methods, this is the key to the stability, but implicit methods are not suitable for periodic conditions and parallelization. We have avoided these problems by introducing an operator named adhesive operator. Figure 2 is the demonstration of the adhesive operator for parallel computing. A quantum wave packet runs over a 2D periodic space, this space was divided into nine areas, and nine computers managed each areas.
 |
 |
Figure 4a and 4b shows a simple simulation of electron flow accelerated by an external electric force. This system is periodically connected so that the the electron can flow forever.
|
| ||
|---|---|---|---|
|
Fig. 4a: Dynamics of the electron density in a periodic 2D system. The electron starts flowing by the external electric force. |
Fig. 4b: Dynamics of the electron current in the same system. These segments show the current density, and "red" and "green" mean left-turn and right-turn vortexes respectively. | ||
We introduced a concept of a finite element method (FEM) for the real space time evolution method. It was found that by using FEM, the accuracy are dramatically improved without the increase of the computational effort.
Figure 5 shows a simple comparison of the accuracy of these methods. The evolution of a Gaussian wave in 1D system is computed by an ordinally finite differential method and the finite element method respectively.
 |
It is very important to improve the real space time evolution method to manage systems under external magnetic fields. The Schroedinger equation in such systems involves a vector potential, which made the computation very troublesome. We formulated an efficient algorithm to computer the evolution under a magnetic field.
Figure 6 shows a cyclotron motion of an electron in a static magnetic field. The motion of the expected value of the positions agreed with the classical result.
 |
Figure 7 shows Aharonov-Bohm effect. The interference pattern is shifting with the increase of the magnetic flux.
 |
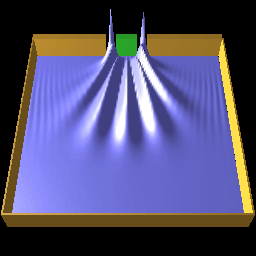Figure 8 shows the dynamics of a quantum wave packet in a 2D system applied with both electric force and magnetic force.
 |
We have confirmed the our method for the TD-Schroedinger equation is also useful for the TD-Khon-Sham equation, namely, the dynamics of many-body systems.
Figure 9 shows a simple simulation, collision of two electrons.
 |
For the performance test of the method in realistic systems, we simulated an electron dynamics in a hydrogen atom in a strong laser. Figure 10a shows the time evolution of the electron density during the electron excitation. We found the state gradually turns from the 1S-orbital to the 2P-orbital.
 |
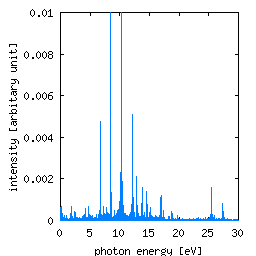
Fig. 10b: Spectrum of the scattering light.
It is remarkable that by using our real space computations, we can start the simulation only with the Hamiltonian and the initial state. In other words, we do not need the informations about the excited states to start the simulation. However, we can find the informations about the excited states by simulating the time evolution.
Those simulations above treat only one electon. Then, we have simulated atom excitations of H, He, and Be atoms. We have extended our method to many-body systems; TD-Kohn-Sham equation. We have found that even though the effective potential in TD-KS evolves by itself, the simulation can be performed naturally, without any complicated procedures.
Figure 11 shows the excitations of each atoms. In these systems, the core potential is treated by bare coulomb potential except the singular point.
 |
 |
 |
Next, we have applied our method to a molecule; methane. Figure 12 shows the motion of electrons density around a methane molecule. A strong pulse laser is applied to this molecule at t=0, so that the electrons are kicked, and start vibration.
 |
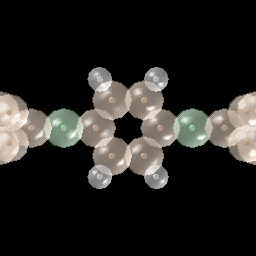
Figure 13 shows another kind of simulation. The molecule is benzene. An increasing magnetic field is applied perpendicular to this molecule. An induced electric field accelerates the electrons motion, and electrons start flowing around this ring molecule.
 |
Next, we have simulated a periodic system; diamond crystal. A pulse laser was applied at t=0, then we followed the motion of electrons density. In this simulation, we considered the effect of anti-electric field. As a result, we could see the plasmon in this crystal.
 |
Next, we have simulated a partially periodic system; Carbon graphite. In this system, it is periodic in xy plane, but isolate in z axis. We can treat such complicated boundary conditions by using real space approach. Figure 14 shows the motion of electrons around the graphite. it was moved by a pulse laser. but it never flows.
 |
The next simulation is much more complicated than ever. Figure 16 shows the electron motion around carbon nano-tube (4,4). There are 20 carbon atoms, 80 electrons, and 40 orbitals in a unit cell. These electrons flows around the tube due to the increasing magnetic field applied to this tube.
 |
The last simulation is more complicated, C60 fullerene. Figure 17 shows the electron motion. There are 60 carbon atoms, 240 electrons, and 120 orbitals. These electrons moved by a strong laser applied to this large molecule.
 |
Finally, we show some our future dream. By using our method, it will be possible to examine the nonlinear optical property of atoms. The simulation of electrons flow in mesoscopic devices will be important near future to design such systems. Also, the analysis of electrical switching property of molecular devices will be important in the future industry.
 |
 |
 |
