時間発展する電子状態の第一原理シミュレーション法の開発
渡辺 尚貴
電子状態の第一原理計算とは、通常は
対象とする系のSchroedinger方程式を解いて、
最もエネルギーの低い固有状態の波動関数とエネルギーを計算する
作業のことです。量子力学の基礎方程式に従った理論計算で
物質の物理特性を解明することが目的です。
Schroedinger方程式そのままでは解くべき波動関数が
非常に複雑になるので、これを簡略化できることを正当化した
密度汎関数理論のKohn-Sham方程式で一電子波動関数と一電子エネルギーを
計算することがほとんどです。
それでも、ちょっと大きな系の第一原理計算を行うには
かなりの計算資源と計算技術が必要です。
以前は第一原理計算するだけで博士号がとれると言われた程です。
最近はコンピュータの性能向上にスパコンの普及、
それに第一原理ソフトの改良と普及のおかげで、
初学者でも第一原理計算を行うことができます。
もちろん計算する対象を選ぶセンスや
計算結果から物理を引き出す能力が必要なことは言うまでもありません。
電子状態の定常的な基底状態の第一原理計算については
すでに多くの計算技術と計算例があります。
計算物理学としてはほぼ完成した道具となり、改良の余地は
少ないと思います。もちろん電子相関をより正しく計算する方法
を作らないとなりませんが、それは密度汎関数理論とは根本的に
異なる研究課題です。
次世代の第一原理計算として、時間依存 Schroedinger方程式や
時間依存 Kohn-Sham方程式にもとづいて電子状態の時間発展の
数値シミュレーションの研究や応用が始まっています。
波動関数が外場などを受けて時間発展するようすを追跡することで、
従来は摂動論を用いて固有状態の重ね合わせで議論していた
励起状態や応答係数に関する解析をより直接的に解析できます。
また非常に短い時間の間に状態がどう変化するかを
直接観察することができるようにもなります。
ところが、この種の計算は容易ではなく、計算法の改良が急務
となっています。もっとも顕著な例として以下のシミュレーションを
お見せします。マウスカーソルを絵の中に入れると絵が動き始めます。
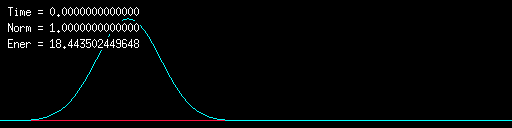
1次元ガウス波束の運動:Euler法で計算しため大失敗となる
このように波束は発散してしまい、計算は破綻します。
波動関数は粒子の存在確率を表すものなので、閉じた空間に
粒子がある場合、確率の空間内での積分は必ず1であることが要求されます。
これは波動関数のノルムが保存されることであり、
これがこのシミュレーションの鉄則です。
ノルム保存を守って時間発展を計算するにはその計算手法が
厳密にユニタリな演算になっていないとなりません。
偏微分方程式の数値計算なので近似は避けられませんが、
ユニタリに関しては厳密であることが要求されます。
1次元系の時間発展に関しては Cayley法と呼ばれる特殊な計算法が
厳密にユニタリな演算になることが知られています。
この方法を使うと先のシミュレーションは劇的に改善されます。
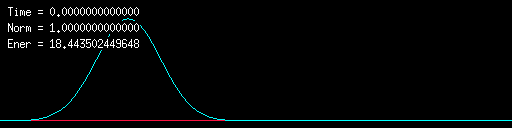
1次元ガウス波束の運動:Cayley法で計算しためノルムも超高精度に保存される
ノルムは見る限り厳密に保存されています。もちろん数値計算なので
数値的丸め誤差は避けられません。しかしそれも十分無視できます。
このCayley法の計算はある種の陰解法のため一般には多くの計算量が
必要となるのですが、この計算の場合はEuler法と大差無い程度で
空間の格子点の数に比例した少ない計算量で計算できます。
この計算では波動関数を実空間の格子点で離散化して計算しています。
従来から広く用いられている平面波展開の方法にはそれなりの多くの利点が
あるのですが、フーリエ変換が頻繁に必要となるため、どうしても
計算量が少なくなりませんでした。実空間の格子点なら計算量をより
少なくできる可能性があるのです。残る問題点は計算精度です。
1次元自由系においてもCayley法は近似計算ですが、平面波のフーリエ変換は
可能な限りの最高精度の計算となります。
ところがCayley法に有限要素法のアイデアを用いることができます。
従来それは計算量を増やしてしまい現実的な計算法ではないと
思われていたのですが、それを克服することで、Cayley法にフーリエ変換に
匹敵する精度を備えました。下の動画は差分法のCayley法での
計算結果と有限要素法のCayley法での結果の比較です。
1次元ガウス波束の運動:差分法(FDM)と有限要素法(FEM)の比較
青色の曲線がFDM、赤色の曲線がFEMの確率密度の時間変化を
表し、縦棒が位置の期待値を表します。緑の縦棒が位置の期待値の厳密解であり、
この動画から有限要素法で計算精度が劇的に改善されることが分かります。
この計算法の注目すべき点は有限要素法で計算精度をあげたにもかかかわらず、
計算量は差分法のときと比べてまったく増えていないことです。実空間の
Cayley法が平面波のフーリエ変換を総合的には優位となる可能性があるのです。
ところがこのCayley法は2次元系や3次元系では使えません。
また電場や磁場がある場合はもっと扱いにくくなってしまいます。
そのためCayley法は現実的な計算には不向きと思われていました。
しかし、指数積展開法と呼ばれる
数値シミュレーションの業界で近年注目されている方法を
用いると Cayley法はにわかに活気付きます。
下の動画は2次元メゾスコピック系を模した系で、
外から一様な電場をかけて電子の波束を流れ始めさせようとしています。
 |
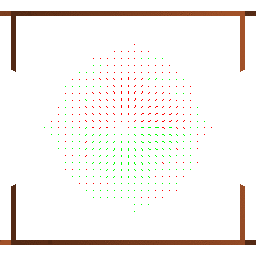 |
| 電子密度の時間発展 | 電流密度ベクトルの時間発展 |
|---|
2次元メゾスコピック系での電子の流れ。左向きの一様電場がある。
この計算からもわかるように電流は渦を作りながら複雑に時間変化します。
この種の計算がCayley法と指数積展開法を用いて非常に簡単に
行えるようになりました。
電場だけでなく、磁場がかかった系の時間発展の計算も
行えます。磁場がある場合、ベクトルポテンシャルがナブラ演算子と
絡まるため計算が少々複雑になるのですが、ここで指数積展開と
ゲージ変換を工夫することで簡単な手順の組合せで磁場下の時間発展の
計算ができるようになりました。
下の動画は2次元メゾスコピック系を模した系で、
外から一様な磁場と電場をかけて電子の波束の運動を観たものです。
 |
 |
| 静磁場下でのサイクロトロン運動 | 静電磁場下での
トロコイダル運動 |
|---|
2次元メゾスコピック系での電子の運動。一様な静磁場と静電場がある。
一様静磁場がある場合、運動していた電子波束は
サイクロトロン運動と呼ばれる円運動をします。その様子がはっきりと
わかります。さらに電場と磁場がある場合には円運動の中心が徐々に
移動して行くトロコイダル運動となります。興味深い点は
波束が決して拡散せずに、まとまり続けながら時間発展していくことです。
これには磁場下におけるランダウ準位の存在が影響しています。
指数積展開法の理論は静的なハミルトニアンだけでなく
動的なハミルトニアンにも適応できます。つまり、光のように時間変化する
電場においての系の時間発展も計算できます。
下の動画は3次元の箱の中に水素原子を置いたもので、この系に
レーザー光線を模した非常に強い振動電場をかけています。
水素原子の光励起。1Sと2Pzの間の励起振動が観察される。
始め1S状態にあった確率分布が、振動電場にひかれて徐々に2Pz状態に
遷移して行く様子が観察できます。そしてその後1S状態に戻り再び
2Pz状態に遷移して行くRabi振動が観察されます。
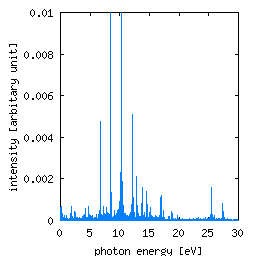
このような振動電場における原子の分極の時間振動を解析することによって
原子のあらゆる光応答特性を求めることができます。非線形光学応答特性
も自然に求めることができます。上の右図は計算の結果得られた
散乱スペクトルで種々の非線形効果による輝線ピークが見出されています。
次に多電子の時間発展を計算するために、これまでに1電子用に開発してきた
計算手法を時間依存 Kohn-Sham方程式に適応することを試みました。
この方程式ではハミルトニアン自身が電子密度の汎関数として
時間変化するため、精度良く安定に計算するためには
特別な対処法が必要になると思われていました。
ところがその心配は実は不要で、計算は簡単に行えることが分かりました。
下の動画はそれぞれ H, He, Be原子の光励起の様子を
表しています。これらの計算では原子核のポテンシャルは中心を適当に
丸められたものを使っています。
強レーザー下での原子の光励起過程: (a) H, (b) He, (c) Be.
次に、この計算法を分子に適応してみました。原子核のポテンシャルには
擬ポテンシャルを用いています。ノルム保存型の非局所擬ポテンシャルでも
ノルムを保存しながら時間発展することができます。
下の動画は
メタン分子での電子の運動を表しています。
強力なパルスレーザーが最初に照射され、電子が蹴飛ばされ、
その後の振動を観察できます。
パルスレーザーによるメタン分子の電子の振動
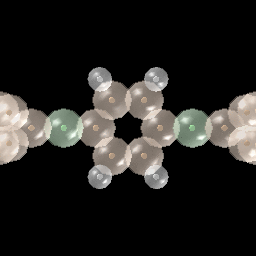
下の図はベンゼン分子での電子の運動を表しています。
時間とともに増加する磁場をこの分子面に垂直に照射しています。
すると誘導起電力が生じるので、この環状分子内に渦電流が流れ始めます。
時間増加磁場により誘起されたベンゼン分子での渦電流
次に、結晶で同様にパルスレーザーを照射する計算を試みます。
結晶と分子の大きな違いは周期性です。周期性のため電場の
扱いが大きく異なり、さまざまな注意点が生じます。
それらを総合すると結晶中に生じるプラズマ振動を見ることができます。
下の動画はダイアモンド
結晶にパルスレーザーを照射し、反電場の効果も含めて電子振動を
再現したものです。
ダイアモンドのプラズマ振動
下の図はグラファイトシートにシートに沿って電場を
かけた計算結果です。
この系ではXY平面で周期的ですが、Z軸方向では孤立的です。
そのような込み入った境界条件でも、実空間法なら柔軟に対処することができます。
グラファイトシートでの電子運動
下の動画はより複雑なシミュレーションの例で、
カーボンナノチューブでの電子運動を表します。
チューブの軸に平行に時間とともに増加する磁場を照射することで、
チューブの輪にそって誘導起電力を生じさせ、渦電流を生じさせています。
カーボンナノチューブでの渦電流
下の動画はC60フラーレンでの電子運動です。
ここには120個の電子軌道があり、パルスレーザーによって誘起された
電子振動を見ることができます。
C60フラーレンの電子振動
このようにいろいろな状況下での電子状態の時間発展を
シミュレーションできるようになりました。この数値計算の技術を用いれば
下の動画に模式図で表したようなシミュレーションを行うことができ、
それぞれ原子の強いレーザーによる非線形光学応答、
メゾスケールの量子デバイスでの超高速な電子の流れ、
分子で構成された分子デバイスの動的伝導特性などの研究が可能になると思います。
これら開発したシミュレーション技術とプログラムを用いて
近い将来の産業を発展させていきたいと我々は考えています。
この研究に付いて数式も交えてより
詳しく知りたい方は 博士論文審査会発表資料 を御覧ください。
略歴
- 1998年3月 東京大学 理学部 物理学科 卒業
- 2000年3月 東京大学大学院 理学系研究科 物理学専攻 修士課程 卒業
- 2003年3月 東京大学大学院 理学系研究科 物理学専攻 博士課程 卒業
大学院在学時の研究活動 1998年4月--2003年3月
- 学術論文
-
N. Watanabe and M. Tsukada:
Fast and stable method for simulating quantum electron dynamics, Physical Review E,
Vol 62, No 2, 2914, (2000).
You can obtain the paper from physics/0011068
-
N. Watanabe and M. Tsukada:
Finite element approach for simulating quantum electron dynamics in a magnetic field, J. Phys. Soc. Japan, Vol 69, No 9, 2962, (2000).
You can obtain the paper from physics/0011069
-
N. Watanabe and M. Tsukada: Efficient method for simulating quantum electron dynamics under the time dependent Kohn Sham equation, Physical Review E, Vol 65, No 3, 036705 (2002).
You can obtain the paper from physics/0112015
- Naoki Watanabe:
Fast and stable computational method for simulating time development of wavefunctions (Master thesis, 2000年3月)
- Naoki Watanabe:
Method of first-principles numerical simulation for time-evolving electronic state (Doctor thesis, 2003年3月)
- 国際会議(招待講演)
- N. Watanabe and M. Tsukada:
Fast and stable method for simulating quantum electron dynamics, Riken symposium on Large scale calculation of electronic state (RIKEN, Wakoh, Japan, Nov 4-5, 1999).
- N. Watanabe and M. Tsukada:
Computational techniques for Quantume Electron Dynamics, First conference of Asian Consortium for Computational Materials Science (Jawaharlal Nehru Centre for Advanced Scientific Research, and Indian Institute for Science, Bangalore, India, Nov 29-Dec 1, 2001).
- 国際会議(一般講演)
- N. Watanabe and M. Tsukada:
Fast and stable method for simulating quantum electron dynamics, The 5th International Conference on Computational Physics (Ishikawa Prefectural Industrial Center, Kanazawa, Japan, Oct 11-13, 1999).
- N. Watanabe and M. Tsukada:
Efficient algorithm for TD-Schroedinger equation and TD-Kohn-Sham equation,
International Conference on Computational Physics 2000 (Hyatt Regency Sanctuary Coave, Gold Coast, Queensland, Australia, Dec 3-8, 2000).
- N. Watanabe and M. Tsukada:
Algorithm for simulating time-evolution of wavefunctions under
Time-Dependent Kohn-Sham equation,
Computational Science Workshop 2001 (Epochal Tsukuba International Congress Center, Tsukuba, Japan, Mar 11-13, 2001).
- N. Watanabe and M. Tsukada:
Computational approach for Quantum Electron Dynamics in Nano structures,
APS March meeting (Indianapolis convention center, Indianapolis, USA, Mar 18-22, 2002).
- 国内会議(招待講演)
- 渡辺 尚貴、塚田 捷:
波動関数の時間発展の高速で安定な計算法、計算物質科学フォーラム研究会 (日本大学、1999年11月19-20日)。
- 国内会議(一般講演)
- 渡辺 尚貴、塚田 捷:
波動関数の時間発展の高速で安定な計算法、物性研短期研究会「物性研究における計算物理 -- 新しいアルゴリズムと超大型計算」 (物性研、1999年6月14--16日)。
- 渡辺 尚貴、塚田 捷:
波動関数の時間発展の高速で安定な計算法、日本物理学会1999年秋の分科会 (岩手大学、1999年9月24-27日)。
- 渡辺 尚貴、塚田 捷:
時間依存Kohn-Sham方程式の高速で安定な計算法、日本物理学会2000年春の分科会 (関西大学、2000年3月22-25日)。
- 渡辺 尚貴、塚田 捷:
時間依存Kohn-Sham方程式による多電子系の動力学計算、日本物理学会2000年秋の年会 (新潟大学、2000年9月22-25日)。
- 会議抄録
- N. Watanabe and M. Tsukada:
Fast and stable method for simulating quantum electron dynamics, RIKEN Review No. 29 (Jun, 2000): Focused on Large-scale Calculation of Electronic States (No. 24).
- N. Watanabe and M. Tsukada:
Fast and stable method for simulating quantum electron dynamics, Proceedings of the 5th International Conference on Computational Physics, Progress of Theoretical Physics Supplement No. 138, p115, (2000).
- 渡辺 尚貴、塚田 捷:
波動関数の時間発展の高速で安定な計算法、計算物質科学フォーラム研究会報告書。
- 渡辺 尚貴、塚田 捷:
波動関数の時間発展の高速で安定な計算法、物性研短期研究会「物性研究における計算物理 -- 新しいアルゴリズムと超大型計算」。
- N. Watanabe and M. Tsukada:
Efficient algorithm for TD-Schroedinger equation and TD-Kohn-Sham equation,
Proceedings of the International Conference on Computational Physics,
Computer Physics Communication Vol 142, Iss 2, (2001).
製作/著作 渡辺尚貴
東京大学大学院 理学系研究科 物理学専攻 物性理論 塚田研究室
naoki@cms.phys.s.u-tokyo.ac.jp