第3章波の進行

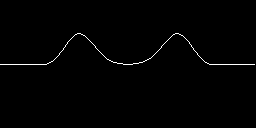
波動力学の簡単な計算例として、下図の様にバネと重りが連なった系を伝わる波を考えましょう。

各重りの平衡点からのずれ y_n の運動方程式は以下の通りです。

解析的な解き方には色々ありますが、数値的にはこの式をそのまま使うだけです。重りの総数をN=256個として、適当な初期条件の元、その時間発展を計算します。

プログラムは作業を関数別にして次のようになります。

//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*
//   Program phonon
//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*

#include <stdio.h>
#include <math.h>
#define  ANIMATION
#include "nxgraph.h"

//---- physical setting
#define N          (256)
#define K          (1.0)
#define M          (1.0)
#define dT         (1.0/16)

//---- graphic setting
#define WIN_WIDTH  (512)
#define WIN_HEIGHT (256)

//---- initialize wave
void Init( double x[N], double p[N] )
{
  for( int i=0 ; i<N ; i++ ){
    x[i] = exp(-0.01*(i-N/2)*(i-N/2));
    p[i] = 0.0;
  }
}

//---- set border conditions on both side edges
void Edge( double x[N], double p[N] )
{
  x[0] = x[N-1] = 0.0;
  p[0] = p[N-1] = 0.0;
}

//---- evolve the system by time 16*dT
void Evolve( double x[N], double p[N] )
{
  int i;

  for( int interval=0 ; interval<16 ; interval++ ){
    for( i=0 ; i<=N-1 ; i++ ){
      x[i] += p[i]/M*dT;
    }
    p[0] += K*( x[1] - x[0] )*dT;
    for( i=1 ; i<=N-2 ; i++ ){
      p[i] += K*( x[i+1] + x[i-1] - 2*x[i] )*dT;
    }
    p[N-1] += K*( x[N-2] - x[N-1] )*dT;
  }
}

//---- draw phonon wave
void Draw( double x[N] )
{
  NXClearWindow();
  NXDrawMoveto( 2*0, WIN_HEIGHT/2 - (int)(128*x[0]) );
  for( int i=1 ; i<N ; i++ ){
    NXDrawLineto( 2*i, WIN_HEIGHT/2 - (int)(128*x[i]) );
  }
  NXFlush();
}


//---- main function
int main(void)
{
  XEvent ev;
  NXOpenWindow("Phonon Wave", WIN_WIDTH, WIN_HEIGHT );

  double x[N], p[N];

  Init( x, p );
  do{
    Edge( x, p );
    Evolve( x, p );
    Draw( x );
    NXCheckEvent( NX_NOWAIT, ev );
  }while( ev.type != KeyPress );

  NXCloseWindow();

  return(0);
}

系の端は固定端としています。Edge関数で何もしなければ自由端になります。Evolve関数ではEuler法で時間発展を計算します。端(i=0,i=N-1)以外の重りの時間発展の計算は単純です。

系の片方の端から強制的に制限波を入れてみましょう。反対で反射した波と干渉して定在波ができあがります。波の進む速度とその波の周波数の関係を調べてみてください。速度は周波数によってわずかに異なります。分散関係です。

第4章電気力線と等電位線

渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp

第3章 波の進行

第3章波の進行