第4章電気力線と等電位線

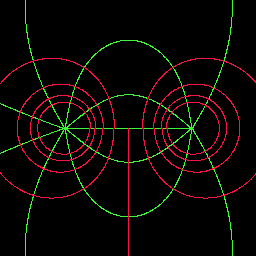
固定されているいくつかの電荷の周りの電気力線と等電位線を計算して描いてみましょう。例として正負2つの電荷が x=-1 と x=+1 に固定されているとします。この電荷が周りに及ぼす静電力は単位系を適当にとることにより次式となります。

電気力線を描くもっとも安直な方法はturtle(亀)法と呼ばれる次の方法です。正の電荷から適当な方向に短い距離進んでみて、そこでの静電力を計算し、その方向に同じ短い距離だけ進む動作を負の電荷に十分近付くか、十分遠ざかるかするまで続けます。

等電位線も適当な所から出発して静電力に垂直に進むことで描かれます。

プログラムは次のようになります。電場の方向を計算する関数 Direction()を用意します。

//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*
//   Program turtle
//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*

#include <stdio.h>
#include <math.h>
#include "nxgraph.h"


//---- physical setting
#define N          (9)            // number of drawing lines
#define dL         (1.0/128)      // turtle's one step
#define dV         (0.5)          // step of volatage

//---- graphic setting
#define WIN_WIDTH  (256)
#define WIN_HEIGHT (256)


double Direction( double x, double y, int& status )
{
  double r1, r2, fx, fy, theta;

  r1 = hypot(x+1.0,y);
  r2 = hypot(x-1.0,y);
  fx = (x+1.0)/(r1*r1*r1) - (x-1.0)/(r2*r2*r2);
  fy = (y)/(r1*r1*r1)     - (y)/(r2*r2*r2);

  theta = atan2( fy, fx );

  if( r2<0.01 || r2>16.0 ){
    status = 1;
  }else{
    status = 0;
  }

  return( theta );
}


//---- main function
int main(void)
{
  XEvent ev;
  NXOpenWindow("Electric line and Volate line", WIN_WIDTH, WIN_HEIGHT );

  int n, flag, status;
  double x, y, theta, V;

  NXSetColor( NXGetColor("green") );
  for( n=0 ; n<N ; n++ ){
    theta = 2*M_PI/N*n;
    x = -1.0;
    y =  0.0;
    NXDrawMoveto( WIN_WIDTH/2+(int)(64*x), WIN_HEIGHT/2+(int)(64*y) );

    while(1){
      x += dL*cos(theta);
      y += dL*sin(theta);
      NXDrawLineto( WIN_WIDTH/2+(int)(64*x), WIN_HEIGHT/2+(int)(64*y) );

      theta = Direction( x, y, status );
      if( status ) break;
    }
  }

  NXSetColor( NXGetColor("red") );
  for( n=0 ; n<N ; n++ ){
    V = dV*(n-N/2);
    x = -V/(1+sqrt(1+V*V));
    y = 0.0;
    NXDrawMoveto( WIN_WIDTH/2+(int)(64*x), WIN_HEIGHT/2+(int)(64*y) );

    flag=0;
    while(1){
      theta = Direction( x, y, status );
      if( status ) break;
      theta += M_PI/2;
      x += dL*cos(theta);
      y += dL*sin(theta);
      NXDrawLineto( WIN_WIDTH/2+(int)(64*x), WIN_HEIGHT/2+(int)(64*y) );
      if( flag==0 && y<0.0 ) flag=1;
      if( flag==1 && y>0.0 ) break;
    }
  }

  NXCheckEvent( NX_WAIT, ev );
  NXCloseWindow();

  return(0);
}

この方法にはさまざまな欠点が在ります。何が欠点なのかを考えて、それらを克服する別な方法を考えてみてください。

第5章磁場中の荷電粒子の運動

渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp

第4章 電気力線と等電位線

第4章電気力線と等電位線