第2章ケプラー運動

ニュートンの万有引力の法則を元に惑星の起動を計算しよう。簡単のため中心の太陽は動かないとして、惑星は1つだけを考えます。惑星の動きは2次元平面内に限定されます。

解析的にこの問題を扱う場合、極座標で考えるのが普通なのですが、単純にデカルト座標で計算することにします。放物運動との違いは働く力が場所によって変わることです。

太陽を原点として、惑星の位置ｑ、運動量ｐの微分方程式は以下のとおりです。

(2-1)

適当な初期値の元、Euler法でこれも数値積分できますが、今回はより精度良く数値積分するためにRunge-Kutta法と呼ばれる別の数値積分法を用いましょう。

惑星運動から離れてRunge-Kutta法の原理をしばらく説明します。ある量 A (スカラーでもベクトルでも可)の時間発展の微分方程式が次のように与えられているとします。

(2-2)

ここでf(A)は既知関数です。t=0でのA(0)からt=dTでのA(dT)を計算することが目的です。

Euler法の解き方は右図の様に t=0でのAの1階微係数からいきなりA(dT)を計算しましたが、もう少し慎重に解くこともできます。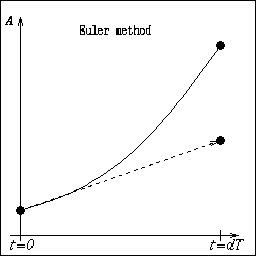

右図と下の式は2次のRunge-Kutta法と呼ばれる数値積分法を表しています。つまりdT/2の中間点でAの1階微係数を求め直してそれを用いてA(dT)を計算するのです。Taylor展開と比較するとdTの2次まで精度があることがわかります。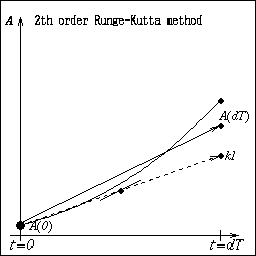

(2-3)

右図と下の式は4次のRunge-Kutta法と呼ばれる数値積分法を表しています。3点の中間点を順次使って求めたA(dT)の暫定値 k1,k2,k3,k4 の重率平均でA(dT)を計算するのです。Taylor展開と比較するとdTの4次まで精度があることがわかります。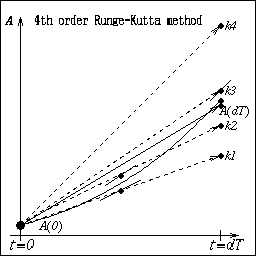

(2-4)

普通、Runge-Kutta法と呼べばこの4次のRunge-Kutta法を指します。

さて、ではRunge-Kutta法を用いて惑星の運動を計算しましょう。まず、単位系を整理します。惑星の円軌道の半径を1天文単位、公転周期を 1年とする長さと時間の単位系を使います。円運動のつりあいの次式から

(2-5)

重力定数 G に太陽の質量 M をかけた値 GM は 4π^2 となることがわかります。惑星の質量は任意に選べますが1とします。時間刻 dTは256分の1年としましょう。

次にRunge-Kutta法の各中間点での微係数からqx,qy,px,pyの暫定値を計算する関数 RungeKutta() を用意します。プログラムは次のようになります

ソースのdownload

//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*
//   Program kepler
//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*

#include <stdio.h>
#include <math.h>
#include "nxgraph.h"

//---- physical setting
#define GM         (4*M_PI*M_PI)
#define M          (1.0)
#define dT         (1.0/256)

//---- graphic setting
#define WIN_WIDTH  (256)
#define WIN_HEIGHT (256)


void RungeKutta( double  qx,  double  qy,  double  px,  double  py,
                 double& qxk, double& qyk, double& pxk, double& pyk )
{
  double q, qi3;
  q   = hypot( qx, qy );
  qi3 = 1.0/(q*q*q);
  qxk = px/M*dT;
  qyk = py/M*dT;
  pxk = -GM*M*qx*qi3*dT;
  pyk = -GM*M*qy*qi3*dT;
}



//---- main function
int main(void)
{
  NXOpenWindow("Kepler Motion", WIN_WIDTH, WIN_HEIGHT );

  double qx=1.0, qy=0.0;
  double px=0.0, py=sqrt(GM)*M;

  double T;
  double qxk[4], qyk[4], pxk[4], pyk[4];

  for( T=0.0 ; T<10.00 ; T += dT ){
    NXDrawPoint( WIN_WIDTH/2 + (int)(64*qx), WIN_HEIGHT/2 + (int)(64*qy) );
    RungeKutta( qx, qy, px, py,
                qxk[0], qyk[0], pxk[0], pyk[0] );
    RungeKutta( qx+0.5*qxk[0], qy+0.5*qyk[0], px+0.5*pxk[0], py+0.5*pyk[0],
                qxk[1], qyk[1], pxk[1], pyk[1] );
    RungeKutta( qx+0.5*qxk[1], qy+0.5*qyk[1], px+0.5*pxk[1], py+0.5*pyk[1],
                qxk[2], qyk[2], pxk[2], pyk[2] );
    RungeKutta( qx+qxk[2], qy+qyk[2], px+pxk[2], py+pyk[2],
                qxk[3], qyk[3], pxk[3], pyk[3] );

    qx += (qxk[0] +  2*qxk[1] + 2*qxk[2] + qxk[3])*(1.0/6);
    qy += (qyk[0] +  2*qyk[1] + 2*qyk[2] + qyk[3])*(1.0/6);
    px += (pxk[0] +  2*pxk[1] + 2*pxk[2] + pxk[3])*(1.0/6);
    py += (pyk[0] +  2*pyk[1] + 2*pyk[2] + pyk[3])*(1.0/6);
  }

  XEvent ev;
  NXCheckEvent( NX_WAIT, ev );

  return(0);
}

Runge-Kutta法の扱いは少々面倒ですが、Eulerより遥かに精度の高い計算ができます。事実、このプログラムは惑星が太陽を10回まわるまで計算するのですが、ずっと同じ楕円軌道を通ります。Euler法では近日点移動(?)が起こってしまいます。

このプログラムを楽しいプログラムに改造するとしたら、例えば太陽の位置をマウスで移動できるようにすると、重力によって惑星の動きを制御できるので、楕円運動について理解が深まります。うまく調整すれば swing byと呼ばれる人工衛星の加速技術を知ることもできます。

第3章波の進行

渡辺尚貴 naoki@cms.phys.s.u-tokyo.ac.jp

第2章 ケプラー運動

第2章ケプラー運動