第1章 放物運動

一様重力場での質点の2次元平面内の運動を計算しましょう。 質点の質量mは1kgとし、 初期条件は位置ｑが原点(qx=0,qy=0)単位は[m]、 運動量ｐが(px=1,py=2)単位は[kgm/s]とします。 この運動方程式は

(1-1)

(1-1)式のｑの2階の微分方程式よりも 次式のｑ,ｐの1階の連立微分方程式の方が微分が簡単で計算も簡単です。

(1-2)

(1-3)

(1-3)式は t=0 まわりでのｑ(dT),ｐ(dT)の Taylar展開で dTの2次以上の 項を完全に無視した非常に粗い近似です。 このように、dTの1次の項しか考えない近似式で微分方程式を 数値的に解くこと方法をEuler(オイラー)法と呼びます。

プログラムでは(1-3)式は次のようになります。

    qx += px/M*dT;
    qy += py/M*dT;
    px += M*0*dT;
    py += -M*G*dT;

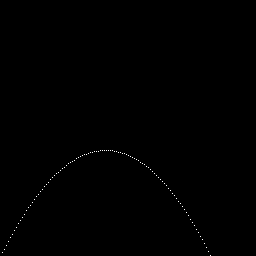
質点が地面より上にある間の軌跡を描くことにしましょう。 次のようになります。

ソースのdownload

//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*
//   Program project
//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*

#include <stdio.h>
#include "nxgraph.h"

//---- physical setting
#define G          (9.80665)
#define M          (1.0)
#define dT         (1.0/256)

//---- graphic setting
#define WIN_WIDTH  (256)
#define WIN_HEIGHT (256)

//---- main function
int main(void)
{
  NXOpenWindow("Projection Motion", WIN_WIDTH, WIN_HEIGHT );

  double qx=0.0, qy=0.0;
  double px=1.0, py=2.0;

  do{
    NXDrawPoint( (int)(512*qx), WIN_HEIGHT-(int)(512*qy) );

    qx += px/M*dT;
    qy += py/M*dT;
    px += M*0*dT;
    py += -M*G*dT;
  }while( qy > 0.0 );

  XEvent ev;
  NXCheckEvent( NX_WAIT, ev );

  return(0);
}

短い時間幅 dT は256分の1秒としました。do whileループで 位置のy座標 qy が正の間ループを回ることにしています。 位置のプロットの際には(qx,qy)の値は非常に小さいので適当に 拡大して、さらにy軸がwindowでは上下逆なので、それにあわせて変換して からプロットします。 ループを抜けた後はプログラムはwindowがマウスかキーで叩かれるまで 停止します。

放物運動のプログラムはこれだけでできあがりです。 この応用として次のプログラムを作ってみてください。

空気抵抗を考慮した放物運動

速度に比例して逆向きの力を働かせるわけです。軌跡はどう変わるでしょうか。

風が吹く中での放物運動

空気抵抗を考慮した上で質点と風との相対運動を考えます。 強い向かい風では質点は投げられたところより後ろに落ちるでしょう。

地面で跳ね返す。

ボールの運動のように適当な跳ね返り係数で地面で跳ね返させます。 地面との衝突をプログラムで判定する方法や跳ね返り直後の 位置、運動量の設定には少々考察が必要です。