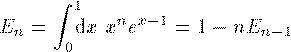 (1)
(1)C言語はUNIX operating systemを設計するためにD.Ritchieらによって 開発された言語体系である。C言語の命令には原始的な操作を行う命令から プロセス制御、ネットワーク制御などの複雑な制御を行う命令までがあり、 柔軟性、移植性にも優れ、多くの種類のマシンやOSで同じソースが使える (グラフィックやシステムコールなどの環境に大きく依存する操作 を含むソースは環境に応じて多少の変更が必要である。)。 そのためC言語はすべての種類のプログラムを設計することができ、 実際、さまざまなプログラムがC言語で設計されてきた。 さらにC言語を基本言語として、オブジェクト指向的な発想で プログラムを設計するためにB.Stroustrupによって開発されたのが C++言語である。
C/C++言語はさまざまな面で従来の言語のFORTRANを圧倒しているが、 物理の研究の最前線では依然FORTRANが優位である。 理由はコンパイラの最適化の性能がFORTRANの方が依然上であるからである。 奇妙に思えるが、この現象は物理屋がFORTRANを使うため、FORTRANの 性能向上の強い要求が出され、コンパイラ開発者がそれに応じている からである。他方、C/C++言語についてはその要求がまだ弱い。
この状況で、将来物理を専攻する学生たちがC/C++言語で プログラムを作り始めることの意義は大きい。それは 将来の計算物理の在り方を変え、コンパイラ開発の状況も変え、 より快適な状況で研究を行えることになるからである。
本書では少しだけC/C++言語の文法を紹介するが、 プログラム言語初心者を教育する目的はない。 その目的の良書はすでに多くあるので、それらに委ねたい。 本書では既習者への簡単な復習の目的でC/C++言語の文法を紹介する。
| 型 | 用途 | サイズ | 範囲 | 精度 |
| char | 文字 | 1byte | -128 〜 +127 | --- |
| short | 小さい整数 | 2byte | -32768 〜 +32767 | --- |
| long | 大きい整数 | 4byte | -2147483648 〜 +2147483647 | --- |
| int | 一般の整数 | 16bit系では shortに同じ、32bit系では longに同じ | ||
| float | 低精度の実数 | 4byte | 0.0, ±1.18×10^{-38} 〜 ±3.40×10^{+38} | 約7桁 |
| ±1.41×10^{-45} 〜 ±1.18×10^{-38} | 7桁以下 | |||
| double | 高精度の実数 | 8byte | 0.0, ±2.23×10^{-308} 〜 ±1.79×10^{+308} | 約15桁 |
| ±4.95×10^{-324} 〜 ±2.23×10^{-308} | 15桁以下 | |||
char 型の変数は、主に文字コードを格納する場合に使われる。
非常に小さい値の整数を格納する場合にも使われる。
short 型と long 型の変数は、それぞれ小さい値の
整数と大きい値の整数を格納する場合に使われる。
int 型の変数はマシンやOS、コンパイラなどの環境によってサイズが
異なる型だが、最近ではほぼ4byteである。
本書では int 型を4byteと見なして整数を扱うほとんどの場合に使う。
float 型の変数は、精度の低い実数を格納する場合に使われる。
double 型の変数は、精度の高い実数を格納する場合に使われる。
本書では実数を扱うほとんどの場合に double 型の変数を使う。
なお、実数の値の範囲はIEEE規格に従ったCPUでの範囲である。異なる規格の
CPUも依然存在する。
char,short,long,int 型に unsigned を冠すると、
非負の整数のみを扱う型になり、
負の整数を扱わない分だけより大きな正の数を扱うことができる。
配列変数は次の様にして宣言する。int a;
要素のindexの取る範囲は0から要素の総数引く1の値までである。 この例では0から9までである。各要素は d[i] で表される。 2次元の配列変数は次の様にして宣言する。double d[10];
後ろの次元の要素がメモリ上で連続して配置される。 2次元配列の後ろの次元の要素数は2の巾乗であることが望ましい。 変数の宣言時に同時に値を代入することができ、それを初期化と呼ぶ。 配列変数でない変数の初期化はただの代入と同じであるが、配列変数では 次の様にして各要素の値を設定することできる。int e[2][4];
double d[10] = { 0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0 };
int e[2][4] = { { 0, 1, 2, 3 }, { 4, 5, 6, 7 } };
3番目の例は 1.6×10^{-19} の定数を表す。 小数点や指数指定を表す e が含まない数の定数は整数と見なされる。a = 1; x = 3.14; y = 1.6e-19;
定数にもその意味が明らかになるように変数のように名前を付けることが できる。以下のように const を使う。
こうして宣言かつ初期化された LIGHT_C は 3.0×10^8 の値を 表す定数の変数となる。これを変数と同じように式中で用いることができる。 複数の箇所に現れる同じ意味の定数をこのような定数の変数で記述して おくと、これらの定数の値の変更は、その初期化の値を変更するだけで済み 大変便利である。const double LIGHT_C = 3.0e8;
constの本来の目的は指定した変数が読み出しにしか使われないことを 表して、コンパイラに種々の最適化を促すことである。 次の例で、変数 a,b に対して、例のように初期化した 変数 c の値は以後変更されないとして扱われる。
定数に名前をつける他の方法に #defineを使う方法がある。 しかし、#define には種々の副作用があるので、 本書では #define は非常に特殊な場合のみに用いることにする。const double c = a+b;
| + | +a として a そのものを表す。 |
| - | -a として a の符号反転を計算する。 |
| * | a*b として積を計算する。 |
| / | a,b どちらかが実数の場合、 a/b として実数の商を計算する。 |
| 整数 n,m の場合、 n/m として整数の商を計算する。 | |
| % | 整数 n,m に対して、 n%m として整数の余りを計算する。 |
| + | a+b として和を計算する。 |
| - | a-b として差を計算する。 |
| = | a=b として b の値を a に上書きする。 |
| += | a+=b として a=a+b を行う。 |
| -= | a-=b として a=a-b を行う。 |
| *= | a*=b として a=a*b を行う。 |
| /= | a/=b として a=a/b を行う。 |
| %= | n%=m として n=n%m を行う。 |
| ++ | 整数 n に対して n++ または ++n として n の値を 1増やす。 |
| -- | 整数 n に対して n-- または --n として n の値を 1減らす。 |
1式中にIncrement/Decrement演算子を他の演算子と共に組み込む場合は この順序則に注意する。n = 1; n = 1; m = (n++)*2; m = (++n)*2;
この様に暗黙のうちに値の型が変換されることもあるが、プログラマが 明示的に値の型を変更することもできる。int n; double a, b; b = a + n;
型名を小括弧 () で囲んだものを変数に冠すると 変数の値は指定した型で扱える限りその型で扱われる (例えば巨大な値の実数は int に変換できず、 プログラムはそこで中断される。)。 変数自体は変更を受けない。これをキャスト演算子と呼ぶ。b = a + (double)n;
キャスト演算子の有効な利用例には、実数 a に対して (int)a と して、 a の値の整数部のみを取り出すことや、整数同士の割算で (double)n/m として、小数も含めた商を計算することなどがある (分子を double 型としたため、暗黙の型変換により分母も 自動的に double 型に変換される。)。
C++言語ではキャスト変換をあたかも関数で行うかのように
とすることもできる。b = a + double(n);
| 関数 prototype | 内容 | 定義域 | 値域 |
| double fabs( double x ) | |x| | [-∞,+∞] | [0,+∞] |
| double sqrt( double x ) | sqrt(x) | [0,+∞] | [0,+∞] |
| double cbrt( double x ) | sqrt[3](x) | [-∞,+∞] | [-∞,+∞] |
| double hypot( double x, double y ) | sqrt(x^2+y^2) | [-∞,+∞] | [0,+∞] |
| double sin( double x ) | sin(x) | (-∞,+∞) | [-1,+1] |
| double cos( double x ) | cos(x) | (-∞,+∞) | [-1,+1] |
| double tan( double x ) | tan(x) | (-∞,+∞) | (-∞,+∞) |
| double asin( double x ) | Arcsin(x) | [-1,+1] | [-π/2,+π/2] |
| double acos( double x ) | Arccos(x) | [-1,+1] | [-π/2,+π/2] |
| double atan( double x ) | Arctan(x) | [-∞,+∞] | [-π/2,+π/2] |
| double atan2(double y, double x) 注1 | Arctan(y/x) | [-∞,+∞] | [-π,+π] |
| double sinh( double x ) | sinh(x) | [-∞,+∞] | [-∞,+∞] |
| double cosh( double x ) | cosh(x) | [-∞,+∞] | [ 1 ,+∞ ] |
| double tanh( double x ) | tanh(x) | [-∞,+∞] | [-1,+1] |
| double asinh( double x ) | Areasinh(x) | [-∞,+∞] | [-∞,+∞] |
| double acosh( double x ) | Areacosh(x) | [ 1,+∞ ] | [-∞,+∞] |
| double atanh( double x ) | Areatanh(x) | [-1,+1] | [-∞,+∞] |
| double exp( double x ) | exp(x) | [-∞,+∞] | [0,+∞] |
| double expm1( double x ) 注2 | exp(x)-1 | [-∞,+∞] | [-1,+∞ ] |
| double log( double x ) | log_e(x) | [0,+∞] | [-∞,+∞] |
| double log10( double x ) | log_10(x) | [0,+∞] | [-∞,+∞] |
| double log1p( double x ) 注2 | log_e(1+x) | [-1,+∞] | [-∞,+∞] |
| double pow( double x, double y ) | x^y | [-∞,+∞] | |
| double rint( double x ) 注3 | x を四捨五入した整数 | [-∞,+∞] | [-∞,+∞] |
| double floor( double x ) 注3 | n ≦ x < n+1 の整数 n | [-∞,+∞] | [-∞,+∞] |
| double ceil( double x ) 注3 | n-1 < x ≦ n の整数 n | [-∞,+∞] | [-∞,+∞] |
| double remainder( double x, double y ) | 余り: x - rint(x/y)*y | [-∞,+∞] | [-∞,+∞] |
| double fmod( double x, double y ) | 余り: x - floor(x/y)*y | [-∞,+∞] | [-∞,+∞] |
として、これら関数の必要な定義が記述されているファイル math.h を取り込み、さらにコンパイルの際に#include <math.h>
と、 -lm オプションを指定して、数学関数の実体が備えられた 数学ライブラリをプログラムに連結しなくてはならない。 double 型には ±∞ を表す特別な値があり、数学関数には それらの値に対する振舞が規定されているので、それなりの答えが 返ってくる。そのため上の表では関数の定義域に ±∞ も含めた。 関数の結果が double 型で扱えない値の場合には ±∞ を 表す値となって返ってくる。上の表では値域に ±∞ も含めた。 しかしながら物理的な計算において、 ±∞ が表れることに なってはならない。gcc -o main main.cc -lm
|
|
|
|---|
コンピュータの内部では文字も数字として扱われる。現在主流の文字と数字の 対応関係はASCII codeであり、文字 a のASCII codeは 97 である。 C言語でASCII codeを得るには 'a' とする。 その値を格納する変数は通常 char 型である。
文字列は文字通り文字の列であるので、 char 型の配列変数に格納して扱う。 配列変数はその宣言の時だけ、各要素を自動的に設定することができる。 文字列配列の初期化は次の様にする。
この右辺の "" で囲まれた文字列は文字列定数である。 文字列定数をこの様に記述すると、文字列の最後にその 文字列の終端を表す特殊な文字 '\0' が自動的に追加される。 この特殊な文字をNULL終端子と呼ぶ。 文字列を格納するために用意する文字列配列のサイズはNULL終端子の 一文字分だけ余計に必要である。配列をもっと大きく用意しても構わない。 そうしてもNULL終端子があるので文字列の長さに変わりは無い。 逆にNULL終端子が無ければ文字列の終りが全くわからない。 特に後述の文字列を操作する関数や文字列を表示する関数は 文字列配列をNULL終端子が見付かるまで読み進むので、これが ないと大変なことになる。char string[20] = "Computer in Physics";
複数の文字列を束ねる配列変数も作ることができる。
char chapter[4][10] = {"Program","Classical","Quantum","Nuclear"};
char* chapter[4] = {"Program","Classical","Quantum","Nuclear"};
どちらの方法でも、ひとつの文字列は chpater[i] で参照できる。
文字列配列の宣言時以外で文字列定数や他の文字列配列の文字列を代入 するには関数 strcpy() を使う。
このように文字列配列の配列名のみを関数に渡す。char string[20]; strcpy( string, "Computer in Physics" );
文字列配列に他の文字列配列の文字列を追加連結するには 関数 strcat() を使う。
2つの文字列配列の内容を比較するには 関数 strcmp() を使う。char string1[20], string2[11]; strcpy( string1, "Computer " ); strcpy( string2, "in Physics" ); strcat( string1, string2 );
if( !strcmp( string1, string2 ) ){ /* identical case */ }
物理計算には必要の無い知識かも知れないが、上記の文字列操作 関数の作業を自力で行う方法を紹介しておく。後述のプログラム文法を 使用しているので、それらを読んでからここを読み返して文字列の 理解を深めてほしい。
文字列の代入操作
方法その1.
char string1[20], string2[8]="Physics";
int i;
for( i=0 ; string2[i]!='\0' ; i++ ){
string1[i] = string2[i];
}
string1[i] = '\0';
文字列の追加操作char string1[20], string2[8]="Physics"; char *ptr1=string1, *ptr2=string2; while( (*ptr1++ = *ptr2++) != '\0' );
int i,j;
for( i=0 ; string1[i]!='\0' ; i++ );
for( j=0 ; string2[j]!='\0' ; i++, j++ ){
string1[i] = string2[j];
}
string1[i] = '\0';
char *ptr1=string1, *ptr2=string2; while( *ptr1 != '\0' ) ptr1++; while( (*ptr1++ = *ptr2++) != '\0' );
printf() 関数の第1引数には書式制御文字列と呼ばれる特殊な 文字列を指定する。これは出力する変数の値をどこにどう配置するかを 指定するものである。そのまま出力する文字も記述できる。 第2引数以降に出力する値の入った変数を並べる。 printf() 関数は出力した文字数を戻り値とする。
書式制御の機能を次の変数を表示させる実例で示す。
左から整数、実数、文字列、文字の例である。 まずもっとも基本的な printf() 関数の使用例と出力結果を載せる。int i=255; double d=3.141592653; char s[32]="Physics"; char c=97;
次は整数の出力桁数の指定や符号、位置の指定である。 上段は正数に対して、下段は負数に対する使用である。printf("i=%d d=%lf s=%s c=%c\n", i, d, s, c ); i=255 d=3.141593 s=Physics c=a%d 指定の整数は10進数でその通りに出力される。
%lf 指定の実数は小数第7桁が四捨五入されて出力される。
%s 指定の文字列はその通りに出力される。
%c 指定の文字は文字コード(ASCII code)に対応する文字が出力される。
次は実数の出力桁と出力形式の指定である。printf("[%5d] [%-5d] [%+5d] [%05d] [% d] [%d]\n", i, i, i, i, i, i ); printf("[%5d] [%-5d] [%+5d] [%05d] [% d] [%d]\n", -i, -i, -i, -i, -i, -i ); [ 255] [255 ] [ +255] [00255] [ 255] [255] [ -255] [-255 ] [ -255] [-0255] [-255] [-255]1列目:表示スペースの右端に揃う。
2列目:表示スペースの左端に揃う。
3列目:表示スペースの右端に揃い、正数に + の記号が付く。
4列目:表示スペースの右端に揃い、空き部に0が埋まる。
5列目:正数に空白が付き左端に揃う。
6列目:標準、左端に揃う。
次は文字列の出力位置と出力数の指定である。printf("[%lf] [%5.3lf] [%7.3lf] [%e]\n", d, d, d, d ); [3.141593] [3.142] [ 3.142] [3.141593e+00]1列目:標準、小数第7桁で四捨五入。
2列目:小数3桁、全体で5桁のみ、四捨五入。
3列目:小数3桁、全体で7桁のみ、空き部に空白が埋まる。四捨五入。
4列目:指数形式
最後に整数の進数の指定である。printf("[%s] [%10s] [%-10s] [%4s] [%10.4s]\n", s, s, s, s, s ); [Physics] [ Physics] [Physics ] [Physics] [ Phys]1列目:標準、左端に揃う。
2列目:表示スペースの右端に揃う。
3列目:表示スペースの左端に揃う。
4列目:表示スペースが小さすぎるので指定が無視される。
5列目:出力数を4文字に限定、表示スペースの右端に揃う。
printf("%d %o %x\n", i, i, i );
255 377 ff
順に10進数、8進数、16進数である。
scanf() 関数の第1引数には printf() 関数と同様の 書式制御文字列を指定する。これはキーボードに打ち込まれた文字列の どこをどの変数に格納するかを指定するものである。 第2引数以降にデータを受け付ける変数を並べる。 ただし、文字列配列以外の変数には直前に & マークを付け、 文字列配列の変数には何も付けないことに注意しなければならない。 scanf() 関数は正常に変数に格納した個数を戻り値とする。 いくつか実例を示す。
下の例は整数2つの単純な入力である。2つの整数はスペースまたはリターンで 適当に区切られていれば良い。
int a, b;
scanf("%d %d", &a, &b );
実数を受け付ける所で、間違って文字列が打ち込まれることに 対処したいならば、scanf() を次のように使う。
double d;
printf("Input a real number (d) : ");
while( scanf("%lf", &d ) != 1 ){
printf("Illigal date format. try again!\n");
rewind(stdin); // discard data left in buffer
}
想定外の入力への対処のために fgets()とsscanf()を使うこともある。 次の例はOSのredirection機能を使って、整数が行ごとに並んだファイルから 整数を読み込む。間違った形式のデータは読み飛ばされることになる。
int a;
char buf[32];
while( fgets( buf, 32, stdin ) != NULL ){
if( sscanf( buf, "%d", &a ) != 1 ) continue;
printf("%d\n", a);
}