第6章 交流回路

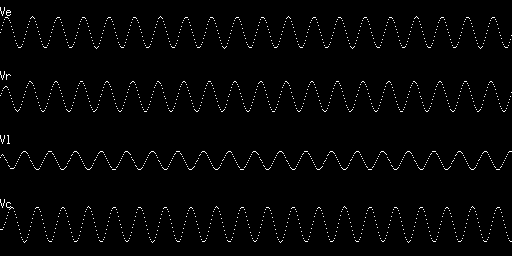
抵抗R、キャパシティC、リアクタンスLの回路に交流電流を 流すとどうなるかをシミュレーションしてみましょう。

交流の起電力が働くRLC直列回路の電流Iの微分方程式は次の通りです。

(6-1)

(6-2)

ソースのdownload

//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*
//   Program rlc
//=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*

#include <stdio.h>
#include <math.h>
#include "nxgraph.h"

//---- physical setting
#define Vo         (1.0)           // amplitude of electric force [V]
#define F          (10.0)          // frequency  [Hz]
#define R          (100.0)         // resistance [ohm]
#define L          (1.0)           // self inductance [H]
#define C          (200e-6)        // capacity   [F]
#define dT         (1.0/256)       // must be much less than 1/F

//---- graphic setting
#define WIN_WIDTH  (512)
#define WIN_HEIGHT (256)

//---- main function
int main(void)
{
  XEvent ev;
  NXOpenWindow("RLC circuit", WIN_WIDTH, WIN_HEIGHT );

  double I=0.0, J=0.0;
  double Ve, Vr, Vl, Vc;
  double T;

  for( int i=0 ; i<WIN_WIDTH ; i++ ){
    T = i*dT;
    J += ( - (1.0/(C*L))*I - (R/L)*J + (2*M_PI*F*Vo/L)*cos(2*M_PI*F*T) )*dT;
    I += J*dT;

    Ve = Vo*sin(2*M_PI*F*T);
    Vr = I*R;
    Vl = J*L;
    Vc = Ve-Vr-Vl;

    NXDrawPoint( i,  1*WIN_HEIGHT/8 - (int)(16*Ve) );
    NXDrawPoint( i,  3*WIN_HEIGHT/8 - (int)(16*Vr) );
    NXDrawPoint( i,  5*WIN_HEIGHT/8 - (int)(16*Vl) );
    NXDrawPoint( i,  7*WIN_HEIGHT/8 - (int)(16*Vc) );
  }
  NXDrawString( 0, 1*WIN_HEIGHT/8-16, "Ve" );
  NXDrawString( 0, 3*WIN_HEIGHT/8-16, "Vr" );
  NXDrawString( 0, 5*WIN_HEIGHT/8-16, "Vl" );
  NXDrawString( 0, 7*WIN_HEIGHT/8-16, "Vc" );

  NXCheckEvent( NX_WAIT, ev );
  NXCloseWindow();

  return(0);
}

位相のずれがわかります。正弦波以外の起電力を働かせてみて どうなるか調べてみましょう。他の回路もいろいろ試してみましょう。