● グラフィック(XWindow System利用者向け)

数字や文字が画面にでてくるだけではいまいち面白くありません。 この章では UNIX-XWindowシステムで計算結果をグラフィックに簡単に描く 方法を紹介します。MS-Windowsシステムでは全く利用できません。

この章で紹介するグラフィックプログラムはグラフィック入門用として 特別に用意したものなので、応用はあまり効きません。

■ Xlib関数代行呼出ライブラリ nxgraph.h

UNIX-XWindowシステムでグラフィックを描くには Xlibと呼ばれる 基幹ライブラリが提供する関数を使うのですが、Xlibの関数にはいろいろ 細かい指定が可能なので豪華なグラフィックも描くことができるのですが、 簡単な図形を描く目的には、Xlibの関数を使うのはやや面倒です。 そこで、Xlibの関数の複雑な呼び出しを自動的に行ってくれる代行呼び出し 関数をいくつか用意して、ファイル nxgraph.h に header file として 用意しました。このファイルを自分のプログラムから #include "nxgraph.h" とすることでこれらの代行呼び出し関数を利用することができます。

nxgraph.h が提供する描画機能は基本的な描画ばかりですので、 もっと豪華なグラフィックプログラムを作りたいなら、 本書後半のXグラフィックの部や市販のXlibの本を読んで学んでください。

nxgraph.hのダウンロード

nxgraph.hに関するもう少し詳しい解説

■ 花びらカオス図形を描くプログラム flower.cc

nxgraph.h の利用例として花びらカオス図形を描くプログラム flower.cc を紹介します。ダウンロードされるか コピーアンドペーストされるかしてファイルに保存してください。

flower.ccのダウンロード

flower.ccの内容

// flower.cc

#include <stdio.h>
#include <math.h>
#include "nxgraph.h"


//---- 指定のパラメータでフラワーカオスを描く関数
void Draw_Flower( double a )
{
  double kx = 8.0*sqrt(2.0+a);
  double ky = 8.0*sqrt(2.0-a);
  double  x = 1.0, y = 0.0;
  double nx, ny;
  int n;

    // 65536回連列を辿る 
  for( n=1 ; n<65536 ; n++ ){
      // 点を描く 
      // 対称性良く描くために座標に一次変換を施します 
    NXDrawPoint( (int)((y+x)*kx)+256, (int)((y-x)*ky)+256 );

      // 次の点を計算する 
    nx = a*x + y + 5.0/(1.0+x*x);
    ny = -x;
     x = nx;
     y = ny;
  }
}


int main(void)
{
  double a;

   // ウィンドウを開く 
  NOpenWindow( "flower chaos", 512, 512 );

   // 描く色を明るいピンク色にする 
  NXSetColor( NXGetColor("light pink") );


  printf("Flower chaos.\n");
  printf("If you input 0, then this program quits.\n\n");

   // aに 0を代入するまで繰り返す 
  while(1){
    printf("Input a double number from -1.5 to +1.5. :");
    scanf("%lf", &a );
    if( a==0 ) break;

      // 図を描く 
    NXClearWindow();
    Draw_Flower( a );
  }

    // ウィンドウを閉じる 
  NXCloseWindow();

  return(0);
}

▲ プログラムのコンパイル

gcc -o flower flower.cc -I/usr/X11R6/include -lX11 -L/usr/X11R6/lib -lm

gcc -o flower flower.cc -I/usr/openwin/include -lX11 -L/usr/openwin/lib -lm

▲ プログラムの実行

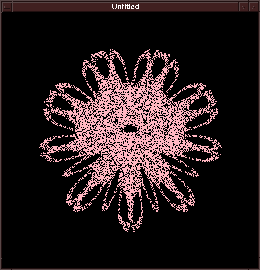
プログラムを実行すると、真っ黒なウィンドウが表れます。 プログラムを実行したところ(例えばkterm)に、種々のメッセージが 表示され、小数の入力されるのを待っています。ここに一つの 小数を入力してリターンキーを押してください。ウィンドウにピンク色で 花びら模様が描かれます。描き終ると、プログラムは小数が入力されるのを また待ちます。先程入力した値とは異なる値を入力してみてください。 別な形の花びら模様が描かれるでしょう。
0を入力するとこのプログラムを終了するようになっています。

▲ 花びらカオス図形の解説

この花柄の絵は数学的な計算により描かれています。 次の2次元の点列の漸化式を考えます。

x[0] = 1.0;
y[0] = 0.0;

x[n+1] = a*x[n] + y[n] + 5.0/(1.0+x[n]*x[n]);
y[n+1] = -x[n];

パラメータ aは -1.5から+1.5の範囲にある適当な実数の定数です。 この点列の漸化式により、各nでの点の位置を次々に計算して その位置を画面にプロットしていくと、このような花びらの図形が 描かれるのです。

この点列の漸化式による点の移動の性質は、漸化式の非線形効果に より非常に複雑になります。そのため点の初期位置に対して、十分 大きなnでの点の位置がまったく予測不能になります。ですがその点は まったくでたらめな位置にあるのではなく、ある決まった範囲内に 必ずあります。これがカオスと呼ばれる現象の際だった特徴です。
この決まった範囲とは、この漸化式では花びらのような図形になる のは不思議なことです。